题目内容
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
【答案】(1)![]() (2)m≤﹣
(2)m≤﹣![]() 或m≥1.
或m≥1.
【解析】试题分析:(Ⅰ)分三种情况讨论,分别求解不等式组,然后求并集即可得结果;(Ⅱ)原不等式等价于f(x)min≤|3m+1|,求出![]() 的最小值,解关于
的最小值,解关于![]() 的不等式,即可得结果.
的不等式,即可得结果.
试题解析:解:(Ⅰ)不等式f(x)<8,即|2x+3|+|2x﹣1|<8,
可化为①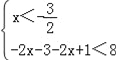 或②
或②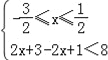 或③
或③ ,…
,…
解①得﹣![]() <x<﹣
<x<﹣![]() ,解②得﹣
,解②得﹣![]() ≤x≤
≤x≤![]() ,解③得
,解③得![]() <x<
<x<![]() ,
,
综合得原不等式的解集为{x|-![]() }.
}.
(Ⅱ)因为∵f(x)=|2x+3|+|2x﹣1|≥|(2x+3)﹣(2x﹣1)|=4,
当且仅当﹣![]() ≤x≤
≤x≤![]() 时,等号成立,即f(x)min=4,…
时,等号成立,即f(x)min=4,…
又不等式f(x)≤|3m+1|有解,则|3m+1|≥4,解得:m≤﹣![]() 或m≥1.
或m≥1.

练习册系列答案
相关题目