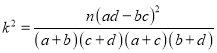题目内容
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
【答案】(1)![]() (2)详见解析(3)
(2)详见解析(3)![]()
【解析】
试题分析:(1)函数f(x)为奇函数,故可得f(x)+f(-x)=0,由此方程求m的值;(2)证明于任意m,f(x)在R上为单调函数,由定义法证明即可,设![]() ∈R,
∈R,![]() ,研究
,研究![]() 的符号,根据单调性的定义判断出结果;(3)因为f(x)在R上为增函数且为奇函数,由此可以将不等式
的符号,根据单调性的定义判断出结果;(3)因为f(x)在R上为增函数且为奇函数,由此可以将不等式![]() 对任意x∈R恒成立,转化为
对任意x∈R恒成立,转化为![]() 即
即![]() 对任意x∈R恒成立,再通过换元进一步转化为二次不等式恒成立的问题即可解出此时的恒成立的条件
对任意x∈R恒成立,再通过换元进一步转化为二次不等式恒成立的问题即可解出此时的恒成立的条件
试题解析:(1)∵![]() ,且
,且![]()
∴![]() (注:通过
(注:通过![]() 求也同样给分)∴
求也同样给分)∴![]()
(2)证明:设![]() ,则
,则![]()
![]()
![]() ∵
∵![]() ∴
∴![]()
∴![]() 即
即![]() 。 所以
。 所以![]() 在R上为增函数。
在R上为增函数。
(3)因为![]() 为奇函数且在R上为增函数,
为奇函数且在R上为增函数,
由![]() 得:
得: ![]()
∴![]()
![]() 对任意
对任意![]() 恒成立。
恒成立。
令![]()
![]() 问题等价于
问题等价于![]() 对任意
对任意![]() 恒成立。
恒成立。
令![]() ,其对称轴
,其对称轴![]()
当![]() 即
即![]() 时,
时,![]() ,符合题意。
,符合题意。
当![]() 时,即
时,即![]() 时,对任意
时,对任意![]() ,
,![]() 恒成立,等价于
恒成立,等价于![]()
解得:![]()
综上所述,当![]() 时,不等式
时,不等式![]() 对任意
对任意![]() 恒成立
恒成立

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】性格色彩学创始人乐嘉是江苏电视台当红节目“非诚勿扰”的特约嘉宾,他的点评视角独特,语言犀利,给观众留下了深刻的印象,某报社为了了解观众对乐嘉的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
男 | 女 | 总计 | ||||||
喜爱 | 40 | 60 | 100 | |||||
不喜爱 | 20 | 20 | 40 | |||||
总计 | 60 | 80 | 140 | |||||
p(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | |||
k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 | |||
(Ⅰ)从这60名男观众中按对乐嘉是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
(Ⅱ)根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱乐嘉有关?(精确到0.001)
(Ⅲ)从(Ⅰ)中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱乐嘉的概率.
附: