题目内容
设关于 的一元二次方程
的一元二次方程 .
.
(1)若 ,
, 都是从集合
都是从集合 中任取的数字,求方程有实根的概率;
中任取的数字,求方程有实根的概率;
(2)若 是从区间[0,4]中任取的数字,
是从区间[0,4]中任取的数字, 是从区间[1,4]中任取的数字,求方程有实根的概率.
是从区间[1,4]中任取的数字,求方程有实根的概率.
(1) (2)
(2)
解析试题分析:(1)设事件A=“方程有实根”,记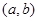 为取到的一种组合,则所有的情况有:
为取到的一种组合,则所有的情况有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4) ……2分
一共16种且每种情况被取到的可能性相同, ……3分
∵关于 的一元二次方程
的一元二次方程 有实根,
有实根,
∴ ……4分
……4分
∴事件A包含的基本事件有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),
(4,2),(4,3),(4,4)共10种, ……5分 ,
,
∴方程有实根的概率是 . ……6分
. ……6分
(2)设事件B=“方程有实根”,记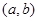 为取到的一种组合,
为取到的一种组合,
∵ 是从区间[0,4]中任取的数字,
是从区间[0,4]中任取的数字, 是从区间[1,4]中任取的数字,
是从区间[1,4]中任取的数字,
∴点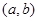 所在区域是长为4,宽为3的矩形区域,如图所示:
所在区域是长为4,宽为3的矩形区域,如图所示: ……9分
……9分
又满足: 的点的区域是如图所示的阴影部分,
的点的区域是如图所示的阴影部分,
∴ ,
,
∴方程有实根的概率是 . ……12分
. ……12分
考点:本小题主要考查古典概型和几何概型.
点评:古典概型要求每个基本事件都是等可能发生的,而几何概型包括与长度、面积、体积、角度等有关的几类问题,要正确区分,灵活转化,仔细计算.

(本小题满分13分)为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处.现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示.
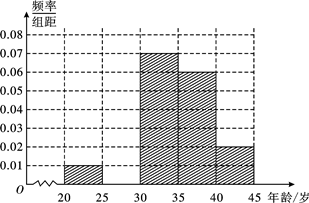
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.05 |
| [25,30) | ① | 0.20 |
| [30,35) | 35 | ② |
| [35,40) | 30 | 0.30 |
| [40,45] | 10 | 0.10 |
| 合计 | 100 | 1.00 |
 的分布列和数学期望;
的分布列和数学期望; (
(
 )
) 从集合
从集合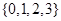 中任取一个元素,
中任取一个元素, 从集合
从集合 恰有两个不相等实根的概率;
恰有两个不相等实根的概率; 中任取一个数,
中任取一个数, 中任取一个数,求方程
中任取一个数,求方程 表示将两件次品被全部检查或推断出来所需检查次数。
表示将两件次品被全部检查或推断出来所需检查次数。 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好,已知某厂执行标准
,产品的等级系数越大表明产品的质量越好,已知某厂执行标准 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下: 的为一等品,等级系数
的为一等品,等级系数 的为二等品,等级系数
的为二等品,等级系数 的为三等品,
的为三等品, ,从该厂生产的产品中任取一件,其利润记为
,从该厂生产的产品中任取一件,其利润记为 ,用这个样本的频率分布估计总体分布,将频率视为概率,求
,用这个样本的频率分布估计总体分布,将频率视为概率,求 ,
, 的概率;
的概率; ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求 的概率.
的概率.