题目内容
已知函数f(x)是R上的偶函数,g(x)是R上的奇函数,且g(x)=f(x-1),若f(1)=2,则f(2 013)的值为( )
(A![]() )2 (B)0 (C)-2 (D)±2
)2 (B)0 (C)-2 (D)±2
A.由g(x)=f(x-1),得g(-x)=f(-x-1),
又g(x)为R上的奇函数,∴g(-x)=-g(x).
∴f(-x-1)=-f(x-1),
即f(x-1)=-f(-x-1).
用x+1替换x,得f(x)=-f(-x-2),
又f(x)是R上的偶函数,
∴f(x)=-f(x+2).
∴f(x)=f(x+4),即f(x)的周期为4.
∴f(2 013)=f(4×503+1)=f(1)=2.

练习册系列答案
相关题目
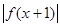 <1
<1 的解集的补集是( )
的解集的补集是( )