题目内容
函数f(x)的定义域为D，若满足①f(x)在D内是单调函数，②存在[a，b]⊆D，使f(x)在[a，b]上的值域为[－b，－a]，那么y＝f(x)叫做对称函数，现有f(x)＝
－k是对称函数，那么k的取值范围是________．
－k是对称函数，那么k的取值范围是________．
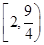
由于f(x)＝－k在(－∞，2]上是减函数，所以
⇒关于x的方程－k＝－x在(－∞，2]上有两个不同实根，通过换元结合图象可得k∈.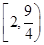
－k在(－∞，2]上是减函数，所以⇒关于x的方程－k＝－x在(－∞，2]上有两个不同实根，通过换元结合图象可得k∈.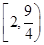
练习册系列答案
阅读快车系列答案
相关题目
，3a＞2c＞2b，求证：
＜－
；
≤|x1－x2|＜
.
定义在区间
都有
且
的值；
且
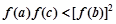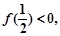求证：
；
求证：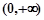
上是增函数.
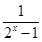是定义在(－∞，－1]∪[1，＋∞)上的奇函数，则f(x)的值域为________．
log2x，若g(x)是f(x)的“拓展函数”，且g(x)是偶函数，则符合条件的一个g(x)的解析式是________．
x－sin x在区间[0,2π]上的零点个数为________．
，为了保证正常用电，安装后采用太阳能和电能互补供电的模式．假设在此模式下，安装后该企业每年消耗的电费C(单位：万元)与安装的这种太阳能电池板的面积x(单位：平方米)之间的函数关系是C(x)＝
(x>0)．记该企业安装这种太阳能供电设备的费用与该企业15年共将消耗的电费之和为F(x)(万元)，则F(40)等于( )