题目内容
设函数f(x)=ax2+bx+c,且f(1)=- ,3a>2c>2b,求证:
,3a>2c>2b,求证:
(1)a>0,且-3< <-
<- ;
;
(2)函数f(x)在区间(0,2)内至少有一个零点;
(3)设x1,x2是函数f(x)的两个零点,则 ≤|x1-x2|<
≤|x1-x2|< .
.
 ,3a>2c>2b,求证:
,3a>2c>2b,求证:(1)a>0,且-3<
 <-
<- ;
;(2)函数f(x)在区间(0,2)内至少有一个零点;
(3)设x1,x2是函数f(x)的两个零点,则
 ≤|x1-x2|<
≤|x1-x2|< .
.(1)-3< <-
<- (2)函数f(x)在区间(0,2)内至少有一个零点.(3)见解析
(2)函数f(x)在区间(0,2)内至少有一个零点.(3)见解析
 <-
<- (2)函数f(x)在区间(0,2)内至少有一个零点.(3)见解析
(2)函数f(x)在区间(0,2)内至少有一个零点.(3)见解析(1)由已知得f(1)=a+b+c=- ,∴3a+2b+2c=0,
,∴3a+2b+2c=0,
又3a>2c>2b,∴a>0,b<0.
又2c=-3a-2b,∴3a>-3a-2b>2b,
∵a>0,∴-3< <-
<- .
.
(2)由已知得f(0)=c,f(2)=4a+2b+c=a-c,
①当c>0时,f(0)=c>0,f(1)=- <0,
<0,
∴函数f(x)在区间(0,1)内至少有一个零点;
②当c≤0时,f(1)=- <0,f(2)=a-c>0,
<0,f(2)=a-c>0,
∴函数f(x)在区间(1,2)内至少有一个零点.
综上所述,函数f(x)在区间(0,2)内至少有一个零点.
(3)∵x1,x2是函数f(x)的两个零点,
∴x1+x2=- ,x1x2=
,x1x2=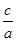 =-
=- -
- ,
,
∴|x1-x2|=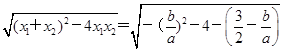 =
= ,
,
∵-3< <-
<- ,∴
,∴ ≤|x1-x2|<
≤|x1-x2|< .
.
 ,∴3a+2b+2c=0,
,∴3a+2b+2c=0,又3a>2c>2b,∴a>0,b<0.
又2c=-3a-2b,∴3a>-3a-2b>2b,
∵a>0,∴-3<
 <-
<- .
.(2)由已知得f(0)=c,f(2)=4a+2b+c=a-c,
①当c>0时,f(0)=c>0,f(1)=-
 <0,
<0,∴函数f(x)在区间(0,1)内至少有一个零点;
②当c≤0时,f(1)=-
 <0,f(2)=a-c>0,
<0,f(2)=a-c>0,∴函数f(x)在区间(1,2)内至少有一个零点.
综上所述,函数f(x)在区间(0,2)内至少有一个零点.
(3)∵x1,x2是函数f(x)的两个零点,
∴x1+x2=-
 ,x1x2=
,x1x2=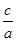 =-
=- -
- ,
,∴|x1-x2|=
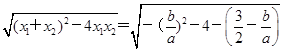 =
= ,
,∵-3<
 <-
<- ,∴
,∴ ≤|x1-x2|<
≤|x1-x2|< .
.
练习册系列答案
相关题目

 若函数y=f(x)-2有3个零点,则实数a的值为( )
若函数y=f(x)-2有3个零点,则实数a的值为( ) ,可继续行驶距离=
,可继续行驶距离= ;
; .
. -k是对称函数,那么k的取值范围是________.
-k是对称函数,那么k的取值范围是________. ,则
,则 = .
= .