题目内容
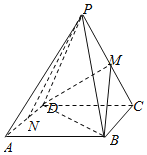
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,侧面
为正方形,侧面![]() 为正三角形,侧面
为正三角形,侧面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)根据题意可证明平面![]() 底面
底面![]() ,由面面垂直的性质可证明
,由面面垂直的性质可证明![]() 平面
平面![]() ;
;
(2)由题意可证明![]() ,则以
,则以![]() 为坐标原点建立空间直角坐标系.写出各个点的坐标,并求得平面
为坐标原点建立空间直角坐标系.写出各个点的坐标,并求得平面![]() 和平面
和平面![]() 的法向量,即可利用法向量法求得两个平面形成二面角的余弦值大小,结合同角三角函数关系式,即可求得求二面角
的法向量,即可利用法向量法求得两个平面形成二面角的余弦值大小,结合同角三角函数关系式,即可求得求二面角![]() 的正弦值.
的正弦值.
(1)证明:∵底面![]() 是正方形,
是正方形,
∴![]() ,
,
∵侧面![]() 底面
底面![]() ,侧面
,侧面![]() 底面
底面![]() ,
,
∴由面面垂直的性质定理,得![]() 平面
平面![]() .
.
(2)设![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,
,
则![]() ,
,![]() .由面面垂直的性质定理知
.由面面垂直的性质定理知![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,故
,故![]() .
.
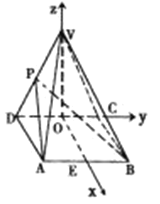
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系
轴正方向,建立如图所示的空间直角坐标系![]() .
.
∵侧面![]() 为正三角形,
为正三角形,
∴![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则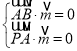 ,即
,即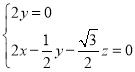 ,即
,即![]() ,
,
所以可取![]() ,
,
平面![]() 的法向量可取
的法向量可取![]() ,
,
于是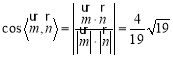 ,
,
由同角三角函数关系式可求得![]()
所以,二面角![]() 的正弦值为
的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机地抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
| ① | ② |
| 0.050 | |
| 0.200 | |
| 36 | 0.300 |
| 0.275 | |
| 12 | ③ |
| 0.050 | |
合计 | ④ |
(1)根据上面的频率分布表,推出①②③④处的数字分别为 , , , .
(2)补全![]() 上的频率分布直方图.
上的频率分布直方图.
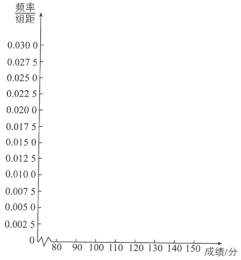
(3)根据题中的信息估计总体:
①成绩在120分及以上的学生人数;
②成绩在![]() 的频率.
的频率.