Question

【题目】设数列是等差数列，数列是各项都为正数的等比数列，且.

（1）求数列，的通项公式；

（2）设，，，试比较与的大小.

Answer 1

【答案】（1）an＝2n﹣1，bn＝3n.（2）当n＝1时，Tn＝2anbn；当n≥2时，Tn＜2anbn.

【解析】

（1）用等差数列和等比数列的基本量法求解；

（2）用错位相减法求和．然后用作差法比较大小．

（1）设等差数列{an}公差为d，等比数列{bn}公比为q.

∵a1＝1，b1＝3，a2+b3＝30，a3+b2＝14，

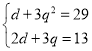∴，化为2q2﹣q﹣15＝0，q＝3（舍去）．

∴q＝3，d＝2.

∴an＝1+2（n﹣1）＝2n﹣1，bn＝3n.

（2）cn＝（an+1）bn＝2n3n，

∴Tn＝2（3+2×32+…+n3n），

3Tn＝2[32+2×33+…+（n﹣1）×3n+n3n+1]，

∴﹣2Tn＝2（3+32+…+3n﹣n×3n+1）＝2（1﹣2n）×3n+1﹣3，

∴Tn.

又2anbn＝2（2n﹣1）×3n.

∴Tn﹣2anbn2（2n﹣1）×3n，

当n＝1时，Tn＝2anbn，

当n≥2时，Tn＜2anbn.