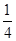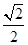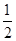题目内容
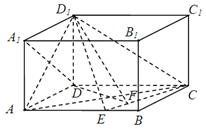
如图,在长方体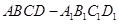 中,
中,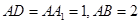 ,点
,点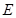 是棱
是棱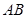 上的一个动点.
上的一个动点.
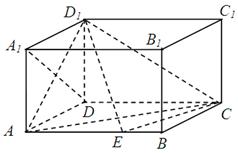
(1)证明: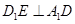 ;
;
(2)当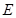 为
为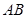 的中点时,求点
的中点时,求点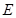 到面
到面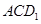 的距离;
的距离;
(3)线段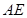 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为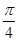 .
.
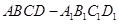 中,
中,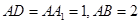 ,点
,点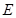 是棱
是棱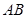 上的一个动点.
上的一个动点.
(1)证明:
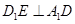 ;
; (2)当
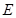 为
为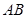 的中点时,求点
的中点时,求点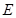 到面
到面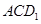 的距离;
的距离;(3)线段
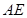 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为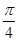 .
.(1)详见解析;(2)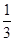 ;(3)
;(3)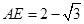 .
.
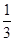 ;(3)
;(3)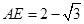 .
.试题分析:解决立体几何中的垂直、距离及空间角,有几何法与空间向量法,其中几何法,需要学生具备较强的空间想象能力及扎实的立体几何理论知识;向量法,则要求学生能根据题意准确建立空间直角坐标系,写出有效点、有效向量的坐标必须准确无误,然后将立体几何中的问题的求解转化为坐标的运算问题,这也需要学生具备较好的代数运算能力.
几何法:(1)要证
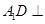
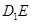 ,只须证明
,只须证明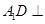 平面
平面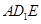 ,然后根据线面垂直的判定定理进行寻找条件即可;(2)运用
,然后根据线面垂直的判定定理进行寻找条件即可;(2)运用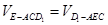 的关系进行计算即可求出点
的关系进行计算即可求出点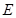 到面
到面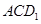 的距离;(3)先作
的距离;(3)先作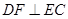 于
于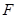 ,连接
,连接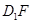 ,然后充分利用长方体的性质证明
,然后充分利用长方体的性质证明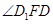 为二面角
为二面角 的平面角,最后根据所给的棱长与角度进行计算即可得到线段
的平面角,最后根据所给的棱长与角度进行计算即可得到线段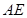 的长.
的长.向量法: (1)建立空间坐标,分别求出
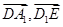 的坐标,利用数量积等于零即可;(2)当
的坐标,利用数量积等于零即可;(2)当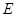 为
为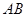 的中点时,求点
的中点时,求点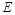 到平面
到平面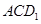 的距离,只需找平面
的距离,只需找平面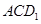 的一条过
的一条过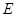 点的斜线段
点的斜线段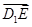 在平面
在平面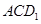 的法向量上的投影即可;(3)设
的法向量上的投影即可;(3)设 ,因为平面
,因为平面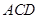 的一个法向量为
的一个法向量为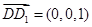 ,只需求出平面
,只需求出平面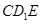 的法向量,然后利用二面角为
的法向量,然后利用二面角为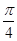 ,根据夹角公式,求出
,根据夹角公式,求出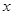 即可.
即可.试题解析:解法一:(1)∵
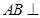 平面
平面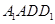 ,∴
,∴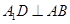 ,又∵
,又∵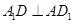 ,
,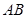 ∩
∩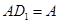 ,∴
,∴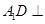 平面
平面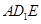 ,
,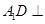
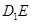 4分
4分(2)等体积法:由已知条件可得,
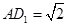 ,
,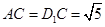 ,所以
,所以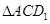 为等腰三角形
为等腰三角形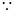
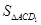 =
=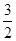 ,
, 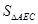
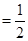 ,设点
,设点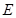 到平面
到平面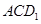 的距离
的距离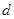 ,根据
,根据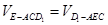 可得,
可得, ,即
,即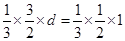 ,解得
,解得 8分
8分(3)过点
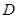 作
作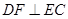 于
于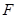 ,连接
,连接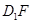
因为
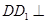 平面
平面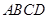 ,所以
,所以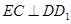 ,又
,又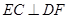 ,
,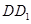 ∩
∩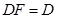 ,所以
,所以 平面
平面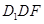
故

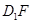 ,
,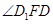 为二面角
为二面角 的平面角
的平面角所以
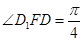 ,
,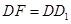
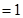 ,
,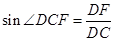
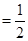 ,
,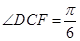 ,
,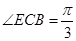
由
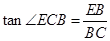 可得
可得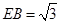 ,
,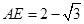 14分
14分解法二: 以
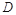 为坐标原点,直线
为坐标原点,直线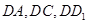 分别为
分别为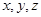 轴,建立空间直角坐标系
轴,建立空间直角坐标系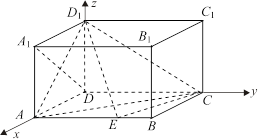
设
 ,则
,则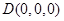 ,
,
(1)
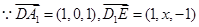 ,
,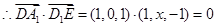 ,故
,故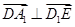 ;
;(2)因为
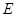 为
为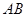 的中点,则
的中点,则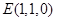 ,从而
,从而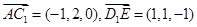 ,
, 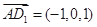 ,设平面
,设平面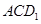 的法向量为
的法向量为 ,则
,则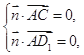 也即
也即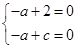 ,得
,得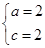 ,从而
,从而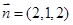 ,所以点
,所以点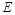 到平面
到平面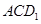 的距离为
的距离为 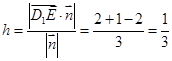 ;
;(3)设平面
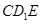 的法向量
的法向量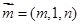 , 而
, 而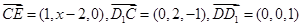 , 由
, 由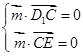 ,即
,即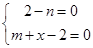 ,得
,得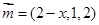 ,依题意得:
,依题意得: 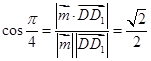 ,
, 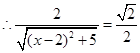 ,解得
,解得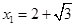 (不合,舍去),
(不合,舍去),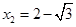
∴
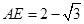 时,二面角
时,二面角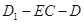 的大小为
的大小为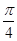 .
. 
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
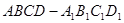 中,
中,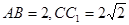 ,
, 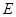 为
为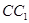 的中点,则点
的中点,则点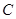 到平面
到平面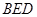 的距离为()
的距离为()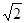
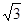
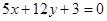 与
与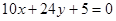 的距离是( )
的距离是( )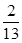
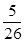
 与圆
与圆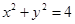 相交于
相交于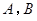 两点,那么弦
两点,那么弦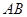 的长等于 ( )
的长等于 ( ) 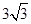
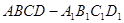 ,下列说法正确的有: ____________.
,下列说法正确的有: ____________.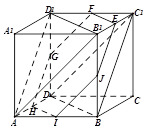
 点在线段
点在线段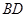 上运动,棱锥
上运动,棱锥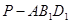 体积不变;
体积不变;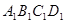 平行;
平行;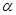 截此正方体,如果截面是三角形,则必为锐角三角形;
截此正方体,如果截面是三角形,则必为锐角三角形;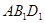 与平面
与平面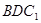 间平行移动时此六边形周长先增大,后减小。
间平行移动时此六边形周长先增大,后减小。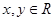 ,则
,则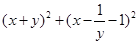 的最小值为( )
的最小值为( )