题目内容
(本题满分10分)
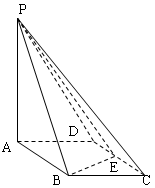
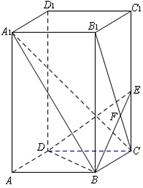
如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
⑴求证:A1C⊥平面BDE;
⑵求A1B与平面BDE所成角的正弦值。
如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,

⑴求证:A1C⊥平面BDE;
⑵求A1B与平面BDE所成角的正弦值。
⑴由三垂线定理可得,A1C⊥BD,A1C⊥BE A1C⊥平面BDE
A1C⊥平面BDE
⑵
 A1C⊥平面BDE
A1C⊥平面BDE⑵

试题分析:⑴由三垂线定理可得,A1C⊥BD,A1C⊥BE
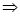 A1C⊥平面BDE
A1C⊥平面BDE⑵以DA、DC、DD1分别为x、y、z轴,建立坐标系,则
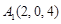 ,
,
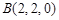 ,∴
,∴ ,
, ∴
∴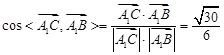
设A1C
 平面BDE=K,由⑴可知,∠A1BK为A1B与平面BDE所成角,
平面BDE=K,由⑴可知,∠A1BK为A1B与平面BDE所成角,∴

点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离的计算。在计算问题中,有“几何法”和“向量法”。本题解法利用了向量,简化了证明过程。

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
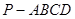 中,
中,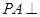 底面
底面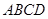 ,
,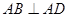 ,
,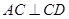 ,
,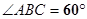 ,
,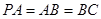 ,
,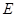 是
是 的中点.
的中点.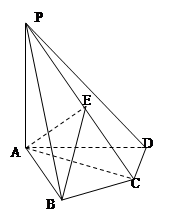
 ;
; 平面
平面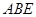 ;
;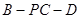 的余弦值.
的余弦值.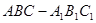 中, AC=4,CB=2,AA1=2,
中, AC=4,CB=2,AA1=2,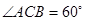 ,E、F分别是
,E、F分别是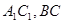 的中点。
的中点。
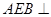 平面
平面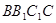 ;
;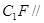 平面ABE;
平面ABE;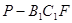 的体积。
的体积。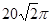
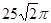
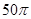
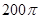
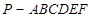 的底面是正六边形,
的底面是正六边形,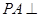 平面
平面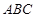 ,
,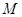 是
是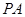 的中点。
的中点。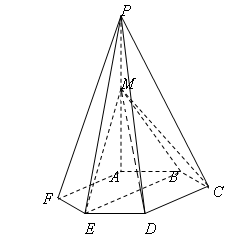
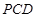 //平面
//平面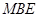 ;
;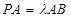 ,当二面角
,当二面角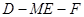 的大小为
的大小为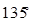 时,求
时,求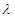 的值。
的值。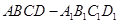 中,
中,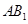 与
与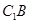 所成的角为( )
所成的角为( )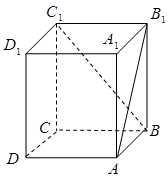

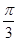
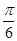
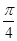
 沿对角线
沿对角线 折成直二面角
折成直二面角 ,有如下四个结论:
,有如下四个结论: ⊥
⊥ 是等边三角形;
是等边三角形; 与平面
与平面 所成的角为60°; ④
所成的角为60°; ④ 所成的角为60°.
所成的角为60°.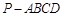 中,
中,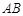 ∥
∥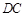 ,
,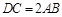 ,
,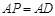 ,
,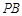 ⊥
⊥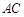 ,
,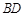 ⊥
⊥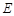 为
为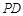 的中点.
的中点.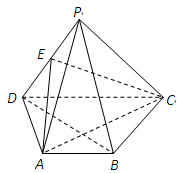
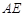 ∥平面
∥平面 ;
;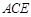 .
.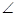 BCD=60
BCD=60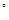 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=2.
底面ABCD,PA=2.