题目内容
(本小题满分12分)
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,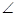 BCD=60
BCD=60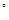 ,E是CD的中点,PA
,E是CD的中点,PA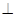 底面ABCD,PA=2.
底面ABCD,PA=2.
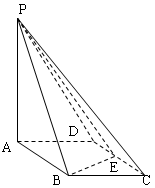
(1)证明:平面PBE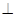 平面PAB;
平面PAB;
(2)求PC与平面PAB所成角的余弦值。
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,
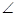 BCD=60
BCD=60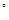 ,E是CD的中点,PA
,E是CD的中点,PA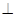 底面ABCD,PA=2.
底面ABCD,PA=2.
(1)证明:平面PBE
 平面PAB;
平面PAB;(2)求PC与平面PAB所成角的余弦值。
(1)利用面面垂直的判定定理来证明。(2) 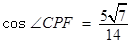
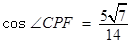
试题分析:(1)略……………………………………………………………………6分
(2)过点C作CF
 AB于F,连接PF。则AF=
AB于F,连接PF。则AF=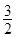
由(1)知
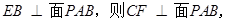
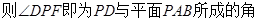 ………………8分
………………8分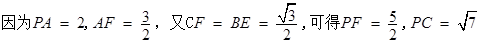 ……10分
……10分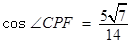 ……12分
……12分点评:对于立体几何中面面垂直的证明,一般可以通过两种方法来得到。几何法,就是面面垂直的判定定理,或者运用向量法来得到,同理对于角的求解也是这样的两种方法,进而反而系得到结论。属于中档题。

练习册系列答案
相关题目
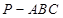 中,
中,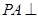 底面
底面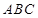 ,
,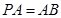 ,
,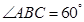 ,
,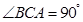 ,点
,点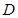 ,
,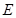 分别在棱
分别在棱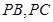 上,且
上,且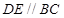
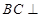 平面
平面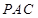 ;
;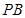 的中点时,求
的中点时,求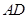 与平面
与平面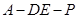 为直二面角?并说明理由.
为直二面角?并说明理由.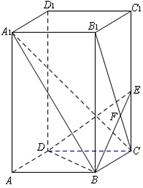
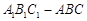 中,侧面
中,侧面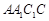
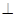 底面ABC,侧面
底面ABC,侧面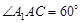 ,E、F分别是
,E、F分别是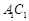 、AB的中点.
、AB的中点.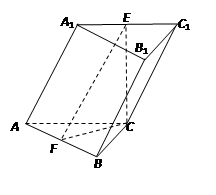
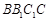 ;
;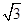 ,VA =" 6."
,VA =" 6." 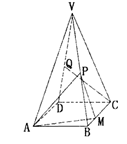
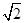 ,F是BC的中点.
,F是BC的中点.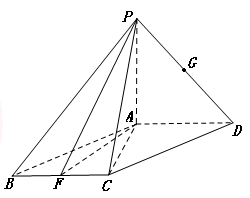
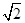 ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
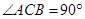 ,
,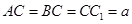 ,
,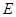 是
是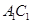 的中点,
的中点,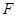 是
是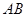 中点.
中点.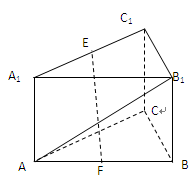
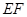 ∥面
∥面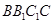 ;
;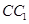 所成角的正切值;
所成角的正切值;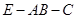 的平面角为
的平面角为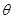 ,求
,求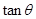 的值.
的值.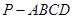 中,侧棱
中,侧棱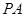 的长为
的长为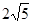 ,
,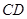 所成的角的大小等于
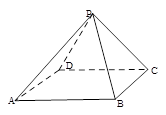
所成的角的大小等于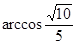 .
.
 的表面上,求此球
的表面上,求此球