题目内容
(本小题满分14分)
如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40 海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20
海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
【答案】
(1)10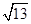 ;(2)该船行驶的速度为10
;(2)该船行驶的速度为10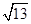 海里/小时,若该船不改变航行方向则会进入警戒水域
海里/小时,若该船不改变航行方向则会进入警戒水域
【解析】
试题分析:(1)如图建立平面直角坐标系:设一个单位为10海里
则坐标平面中AB = 10,AC = 2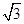 A(0,0),E(0, -4
A(0,0),E(0, -4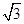 )
)
再由方位角可求得:B(5,5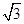 ),C(3,
),C(3,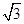 )………………4分
)………………4分
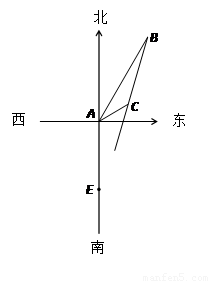
所以|BC|
= 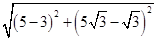 = 2
= 2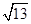
……………6分
所以BC两地的距离为20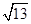 海里
海里
所以该船行驶的速度为10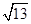 海里/小时
海里/小时
………………7分
(2)直线BC的斜率为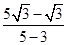 =
2
=
2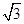
所以直线BC的方程为:y-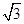 =
2
=
2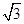 (x-3)
(x-3)
即2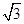 x-y-5
x-y-5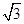 =0………10分
=0………10分
所以E点到直线BC的距离为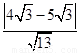 =
=
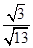 < 1………12分
< 1………12分
所以直线BC会与以E为圆心,以一个单位长为半径的圆相交,
所以若该船不改变航行方向则会进入警戒水域。……………14分
答:该船行驶的速度为10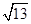 海里/小时,若该船不改变航行方向则会进入警戒水域。
海里/小时,若该船不改变航行方向则会进入警戒水域。
考点:本题考查了直线与圆的实际运用
点评:解直线与圆的问题,要尽量充分地利用平面几何中圆的性质,利用几何法解题要比解析方法来得简捷

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)