题目内容
6.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4)=f(x),且当x∈[0,2]时,f(x)=2x-1,若在区间(-2,6]内关于x的方程f(x)=loga(x+2)恰有3个不同的实数根,则实数a的取值范围是($\root{3}{4}$,2).分析 先利用已知f(x)是定义在R上的偶函数求出在区间[0,2]上的解析式,再利用周期性f(x)=f(x+4)求出函数f(x)在区间[2,4]上的解析式,然后在画出图象,进而求出a的取值范围
解答 解:x∈[0,2],f(x)=2x-1,
∵对任意x∈R,都有f(x)=f(x+4),
∴当x∈[2,4]时,(x-4)∈[-2,0],
∵f(x)是定义在R上的偶函数,
∴f(x)=f(x-4)=2x-4-1;
当x∈[4,6]时,(x-4)∈[0,2],∴f(x)=f(x-4)=2x-4-1.
∵若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0恰有三个不同的实数根,
∴函数y=f(x)与函数y=loga(x+2)在区间(-2,6]上恰有三个交点,
故函数f(x)在区间(-2,6]上的图象如下图所示: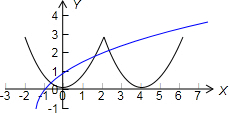
通过画图可知:
恰有三个交点的条件是$\left\{\begin{array}{l}{{log}_{a}^{(6+2)}>3}\\{{log}_{a}^{2+2}<3}\end{array}\right.$,解得 ${2}^{\frac{2}{3}}$<a<2,
即 $\root{3}{4}$<a<2,因此所求的a的取值范围为($\root{3}{4}$,2).
故答案为:($\root{3}{4}$,2).
点评 本题综合考查了函数的奇偶性、周期性、函数的交点及方程的根,熟练掌握函数的性质及数形结合是解决问题的关键.

练习册系列答案
相关题目
1.已知不等式x2-2ax+a<0的解集为∅,则实数a的取值范围是( )
| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (0,1) |
18.已知函数f(x)的定义域为R,且f(x)=f(-x),f(x+1)=-f(x),若f(x)在[-3,-2]上是减函数,$\frac{π}{4}$<α<β<$\frac{π}{2}$,则( )
| A. | f(sinα)>f(sinβ) | B. | f(cosα)>f(cosβ) | C. | f(tanα)>f(tanβ) | D. | 以上都不对 |
14.已知O是△ABC所在平面上一点,满足|$\overrightarrow{OA}$|2+|$\overrightarrow{BC}$|2=|$\overrightarrow{OB}$|2+|$\overrightarrow{CA}$|2,则点O( )
| A. | 在与边AB垂直的直线上 | B. | 在∠A的平分线所在直线上 | ||
| C. | 在边AB的中线所在直线上 | D. | 以上都不对 |
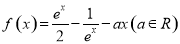 .
.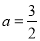 时,求函数
时,求函数 的单调区间;
的单调区间;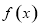 在
在 上为单调函数,求实数
上为单调函数,求实数 的取值范围.
的取值范围.