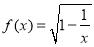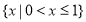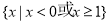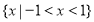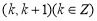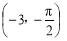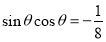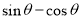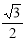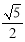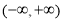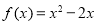题目内容
已知函数 .
.
(1)求函数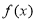 的单调递减区间;
的单调递减区间;
(2)将函数 的图像向左平移
的图像向左平移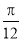 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的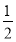 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数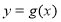 的图像,求
的图像,求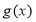 在
在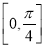 上的值域.
上的值域.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先由正余弦的二倍角公式与辅助角公式化简 ,然后应用正弦函数
,然后应用正弦函数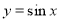 的单调减区间求出函数
的单调减区间求出函数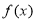 的减区间;(2)用
的减区间;(2)用 代换
代换 得
得 ,然后用
,然后用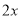 代换
代换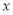 得
得 ,再由
,再由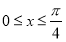 求出
求出 的范围
的范围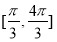 ,最后由正弦函数的性质得出函数
,最后由正弦函数的性质得出函数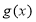 的值域.
的值域.
试题解析:(1)
 4分
4分
由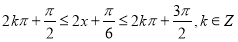 ,解出
,解出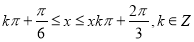
所以 的减区间为
的减区间为 6分
6分
(2)因为将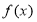 左移
左移 得到
得到
横坐标缩短为原来的 ,得到
,得到 8分
8分

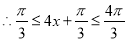

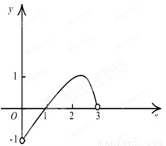
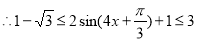 ,所以所求值域为
,所以所求值域为 12分.
12分.
考点:1.三角函数的图像与性质;2.二倍角公式、辅助角公式;3.三角函数的图像变换.

练习册系列答案
相关题目