题目内容
在四面体P-ABC中,PA,PB,PC两两垂直,M是面ABC内一点,M到三个面PAB,PBC,PCA的距离分别是2,3,6,则M到P的距离是( )
| A、7 | B、8 | C、9 | D、10 |
分析:由题意画出图形,M到P的距离是,图形中长方体的对角线的长,求解即可.
解答:解:由于PA,PB,PC两两垂直,M是面ABC内一点,
作出长方体如图,
M到三个面PAB,PBC,PCA的距离分别是2,3,6,则M到P的距离,
就是长方体的体对角线的长:
=7
故选A.
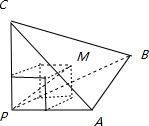
作出长方体如图,
M到三个面PAB,PBC,PCA的距离分别是2,3,6,则M到P的距离,
就是长方体的体对角线的长:
| 22+32+ 62 |
故选A.

点评:本题考查棱锥的结构特征,点、线、面间的距离计算,考查空间想象能力,计算能力,作图能力,逻辑思维能力,是基础题

练习册系列答案
相关题目
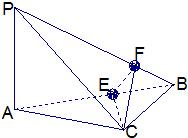 如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2
如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2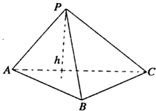 在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则
在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则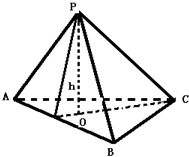 在Rt△ABC中,CA⊥CB,斜边AB上的高为
在Rt△ABC中,CA⊥CB,斜边AB上的高为