题目内容
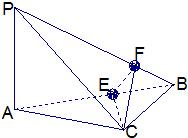 如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2
如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2| 34 |
| 15 |
| 17 |
| 34 |
(1)证明:PB⊥平面CEF;
(2)求二面角B-CE-F的大小.
分析:(1)由题意得EF⊥PB,可根据S△PBC面积的两种表示形式得出CF⊥PB,从而可证得结论.
(2)在平面PAB内,过F作FF1垂直AB交AB于F1,则FF1⊥平面ABC,根据tan∠FEB=cot∠PBA可求得二面角B-CE-F的大小.
(2)在平面PAB内,过F作FF1垂直AB交AB于F1,则FF1⊥平面ABC,根据tan∠FEB=cot∠PBA可求得二面角B-CE-F的大小.
解答:(1)证明:∵PA2+AC2=36+64=100=PC2,
∴△PAC是以∠PAC为直角的直角三角形,同理可证:△PAB是以∠PAB为直角的直角三角形,△PCB是以∠PCB为直角的直角三角形.
故PA⊥平面ABC.
又∵S△PBC=
|AC||BC|=
×10×6=30.
而
|PB||CF|=
×2
×
=30=S△PBC.
故CF⊥PB,又已知EF⊥PB,
∴PB⊥平面CEF.
(2)由(1)知PB⊥CE,PA⊥平面ABC,
∴AB是PB在平面ABC上的射影,故AB⊥CE,
在平面PAB内,过F作FF1垂直AB交AB于F1,则FF1⊥平面ABC,
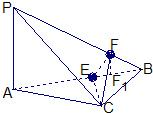
EF1是EF在平面ABC上的射影,
∴EF⊥EC.
故∠FEB是二面角B-CE-F的平面角,tan∠FEB=cot∠PBA=
=
=
,
二面角B-CE-F的大小为arctan
.
∴△PAC是以∠PAC为直角的直角三角形,同理可证:△PAB是以∠PAB为直角的直角三角形,△PCB是以∠PCB为直角的直角三角形.
故PA⊥平面ABC.
又∵S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
而
| 1 |
| 2 |
| 1 |
| 2 |
| 34 |
| 15 |
| 17 |
| 34 |
故CF⊥PB,又已知EF⊥PB,
∴PB⊥平面CEF.
(2)由(1)知PB⊥CE,PA⊥平面ABC,
∴AB是PB在平面ABC上的射影,故AB⊥CE,
在平面PAB内,过F作FF1垂直AB交AB于F1,则FF1⊥平面ABC,

EF1是EF在平面ABC上的射影,
∴EF⊥EC.
故∠FEB是二面角B-CE-F的平面角,tan∠FEB=cot∠PBA=
| AB |
| AP |
| 10 |
| 6 |
| 5 |
| 3 |
二面角B-CE-F的大小为arctan
| 5 |
| 3 |
点评:本题考查了直线与平面垂直的判定及二面角的知识,有一定难度,关键是掌握二面角的求法及直线垂直平面的判定方法.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.
如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.
 ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点, ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
 ,F是线段PB上一点,CF=
,F是线段PB上一点,CF=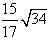 ,点E在线段AB上,且EF⊥PB,
,点E在线段AB上,且EF⊥PB, 