题目内容
【题目】已知直线![]() 半径为
半径为![]() 的圆
的圆![]() 与直线
与直线![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的上方.
的上方.
(1)求圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得弦长等于
截得弦长等于![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)过点![]() 的直线与圆交于
的直线与圆交于![]() 两点(
两点(![]() 在
在![]() 轴上方),问在
轴上方),问在![]() 轴正半轴上是否存在点
轴正半轴上是否存在点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)当点
;(3)当点![]() ,能使得
,能使得![]() 总成立.
总成立.
【解析】
(1)设出圆心![]() 坐标根据直线与圆
坐标根据直线与圆![]() 相切,得到圆心到直线的距离
相切,得到圆心到直线的距离![]() ,确定出圆心
,确定出圆心![]() 坐标,即可得出圆
坐标,即可得出圆![]() 方程;
方程;
(2)根据垂径定理及勾股定理,由过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长等于
截得的弦长等于![]() ,分直线
,分直线![]() 斜率存在与不存在两种情况求出直线
斜率存在与不存在两种情况求出直线![]() 的方程即可;
的方程即可;
(3)当直线![]() 轴则
轴则![]() 轴平分
轴平分![]() ,当直线
,当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 方程为
方程为![]() ,联立圆与直线方程消去
,联立圆与直线方程消去![]() 得到关于
得到关于![]() 的一元二次方程,利用韦达定理表示出两根之和与两根之积,由若
的一元二次方程,利用韦达定理表示出两根之和与两根之积,由若![]() 轴平分
轴平分![]() ,则
,则![]() ,求出
,求出![]() 的值,确定出此时
的值,确定出此时![]() 坐标即可.
坐标即可.
解:(1)设圆心![]() ,
,
因为直线![]() ,半径为
,半径为![]() 的圆
的圆![]() 与相切,
与相切,
![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
则圆![]() 方程为:
方程为:![]() .
.
(2)由题意可知圆心![]() 到直线
到直线![]() 的距离为
的距离为![]()
若直线![]() 斜率不存在,则直线
斜率不存在,则直线![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离为1;
的距离为1;
若直线![]() 斜率存在,设直线
斜率存在,设直线![]() ,即
,即![]() ,
,
则有![]() ,即
,即![]() ,此时直线
,此时直线![]() ,
,
综上直线![]() 的方程为
的方程为![]() 或
或![]() ;
;
(3)当直线![]() 轴,则
轴,则![]() 轴平分
轴平分![]() ,若
,若![]() 轴平分
轴平分![]() ,
,
则![]() ,即
,即![]() ,
,
整理得:![]() ,
,
即![]() ,
,
解得:![]() ,
,
当点![]() ,能使得
,能使得![]() 总成立.
总成立.

【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在头胎生女孩家庭中抽取了5户,进一步了解情况,在抽取的5户中再随机抽取3户,求这3户中恰好有2户生二孩的概率.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
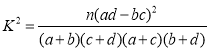 (其中
(其中![]() ).
).