题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点. 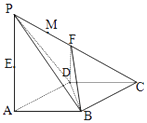
(Ⅰ)证明:PA∥平面FBD;
(Ⅱ)若PA=1,在棱PC上是否存在一点M使得二面角E﹣BD﹣M的大小为60°.若存在,求出PM的长,不存在请说明理由.
【答案】证明:(Ⅰ)连接AC交BD于点O,连接OF, ∵O、F分别是AC、PC的中点,
∴FO∥PA
∵PA不在平面FBD内,
∴PA∥平面FBD
解:(Ⅱ) 解法一:(先猜后证)点M为PC的中点,即为点F,
连接EO,∵PA⊥平面ABCD,
∴PA⊥AC,又∵ABCD是菱形,∴AC⊥BD,
∴BD⊥平面PAC,则BD⊥EO,BD⊥FO,
∴∠EOF就是二面角E﹣BD﹣F的平面角
连接EF,则EF∥AC,∴EF⊥FO,
∵EF= ![]() =
= ![]() ,
,
在Rt△OFE中,tan∠EOF= ![]() =
= ![]() ,
,
故 ![]() ,∴PM=1.
,∴PM=1.
解法二:(向量方法探索)
以O为坐标原点,如图所示,分别以射线OA,OB,OF为x,y,z轴的正半轴,
建立空间直角坐标系O﹣xyz,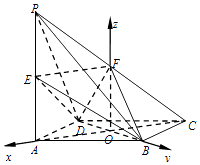
由题意可知各点坐标如下:
O(0,0,0),A( ![]() ,0,0),B(0,
,0,0),B(0, ![]() ,0),D(0,
,0),D(0, ![]() ,0),P(
,0),P( ![]() ,0,1),E(
,0,1),E( ![]() ,0,
,0, ![]() ),
),
设平面EBD的法向量为 ![]() =(x,y,z),
=(x,y,z),
∵ ![]() =(0,1,0),
=(0,1,0), ![]() =(
=( ![]() ,
, ![]() ,
, ![]() ),
),
由 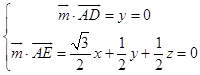 ,取x=1,得
,取x=1,得 ![]() =(1,0,﹣
=(1,0,﹣ ![]() ),
),
设平面BDM的法向量为 ![]() =(a,b,c),点M(x0 , y0 , z0),
=(a,b,c),点M(x0 , y0 , z0),
则由 ![]() ,得M(
,得M( ![]() ﹣
﹣ ![]() ,0,1﹣λ),
,0,1﹣λ),
∴ ![]() =(
=( ![]() ),
), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,1﹣λ),
,1﹣λ),
∴ 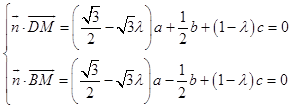 ,取a=1,解得
,取a=1,解得 ![]() =(1,0,
=(1,0, 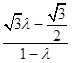 ),
),
由已知可得cos60°= ![]() =
= 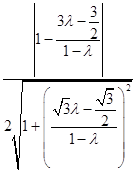 ,解得
,解得 ![]() 或
或 ![]() (舍),
(舍),
∴点M为棱PC的中点.∴PM=1.
【解析】(Ⅰ)连接AC交BD于点O,连接OF,推导出FO∥PA,由此能证明PA∥平面FBD.(Ⅱ) 法一:(先猜后证)点M为PC的中点,即为点F,连接EO,AC⊥BD,BD⊥EO,BD⊥FO,从而∠EOF就是二面角E﹣BD﹣F的平面角,由此能求出PM=1.法二:(向量方法探索)以O为坐标原点,如图所示,分别以射线OA,OB,OF为x,y,z轴的正半轴,建立空间直角坐标系O﹣xyz,利用向量法能求出结果.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案