题目内容
在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积等于
A. | B. | C. | D. |
B
解析试题分析:作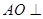 平面
平面 于
于 ,设
,设 ,所以
,所以 为中点,连接
为中点,连接 ,正三棱锥中有
,正三棱锥中有
 平面
平面
 ,
, 平面
平面
 ,在正三棱锥中
,在正三棱锥中

 ,体积为
,体积为
考点:空间几何体线面平行垂直关系的判定及棱锥体积的计算
点评:本题首先由已知条件想到只需求出定点到底面ABC的距离,作出垂线段后利用垂足是中心得到BD与平面ACE的垂直时求解本题的关键点,从而进一步推证侧棱间两两垂直

练习册系列答案
相关题目
正方体的内切球和外接球的半径之比为
A. | B. | C. | D. |
在一个几何体的三视图中,正视图和俯视图如下图所示,则该几何体的体积为( ) 
A. cm3( cm3( | B. cm3 cm3 | C. cm3 cm3 | D. cm3 cm3 |
已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则 ”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若
”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若 的中心为M,四面体内部一点O到四面体各面的距离都相等”,则
的中心为M,四面体内部一点O到四面体各面的距离都相等”,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( ) 

A.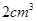 | B. |
C. | D. |





 )可知这个几何体的表面积为( )
)可知这个几何体的表面积为( )




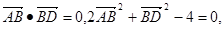 若将其沿BD折起,使平面ABD
若将其沿BD折起,使平面ABD 平面BDC则三棱锥A-BCD的外接球的表面积为:( )
平面BDC则三棱锥A-BCD的外接球的表面积为:( )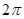



 的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是
的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是



