题目内容
正方体的内切球和外接球的半径之比为
A． | B． | C． | D． |
A
解析试题分析：设正方体的棱长为a，则它的内切球的半径为
，它的外接球的半径为
，所以它的内切球和外接球的半径之比为
考点：本小题主要考查正方体的内切球和外接球的半径之间的关系.
点评：解决此类问题，要注意到正方体的内切球是与正方体的面相切，而外接球的直径是正方体的体对角线.
练习册系列答案
相关题目
若某空间几何体的三视图如图所示，则该几何体的体积是（ ）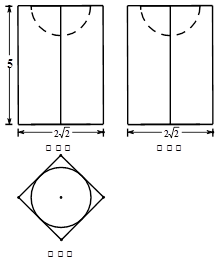
| A．20-2π | B． | C． | D． |
三棱锥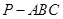
中，
，
， 
⊥底面
，且
，则此三棱锥外接球的半径为
A． | B． | C．2 | D． |
一个几何体的三视图如图所示，则这个几何体的体积为
A． | B．  | C． | D． |
某空间几何体的三视图及尺寸如图1，则该几何体的体积是
A． | B． | C． | D． |
、
、
、
四点，若
，则四面体
的体积的取值范围是
以下对于几何体的描述，错误的是（ ）
| A．以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的旋转体叫做球 |
| B．一个等腰三角形绕着底边上的高所在直线旋转180º形成的封闭曲面所围成的图形叫做圆锥 |
| C．用平面去截圆锥，底面与截面之间的部分叫做圆台 |
| D．以矩形的一边所在直线为旋转轴，其余三边旋转形成的面所围成的旋转体叫做圆柱 |
一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是（ ）
| A．三棱锥 | B．球 | C．圆柱 | D．正方体 |
