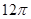已知结论:“在正三角形ABC中.若D是边BC的中点.G是三角形ABC的重心.则 .若把该结论推广到空间.则有结论:“在棱长都相等的四面体ABCD中.若的中心为M.四面体内部一点O到四面体各面的距离都相等 .则A．1B．2C．3D．4 题目和参考答案——青夏教育精英家教网—

题目内容

已知结论：“在正三角形ABC中，若D是边BC的中点，G是三角形ABC的重心，则”。若把该结论推广到空间，则有结论：“在棱长都相等的四面体ABCD中，若的中心为M，四面体内部一点O到四面体各面的距离都相等”，则（）

A．1

B．2

C．3

D．4

解析试题分析：解：设正四面体ABCD边长为1，易求得AM=，又O到四面体各面的距离都相等，所以O为四面体的内切球的球心，设内切球半径为r，则有r=故答案为C
考点：类比推理
点评：本题考查类比推理知识，由平面到空间的类比是经常考查的知识，要认真体会其中的类比方式

练习册系列答案

相关题目

某空间几何体的三视图及尺寸如图1，则该几何体的体积是

已知一个空间几何体的三视图如图所示，则这个几何体的表面积是

如右图是某几何体的三视图，则此几何体的体积是( )

一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的等腰直角三角形,则该几何体的外接球的表面积是 ( )

在正三棱锥A-BCD中，E，F分别是AB，BC的中点，EF⊥DE，且BC＝1，则正三棱锥A-BCD的体积等于

已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是( )

A．	B．
C．	D．

一个球的表面积是，那么这个球的体积为（）

一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形. 则该几何体的表面积为（）

A．16	B．48
C．60	D．96

试题分类