Question

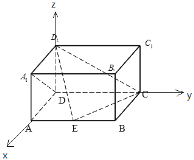
【题目】如图，在长方体ABCD﹣A1B1C1D1中，AD＝AA1＝1，AB＝2，点E在棱AB上移动．

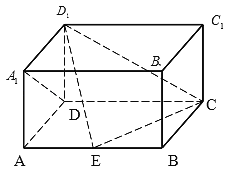
（1）证明：D1E⊥A1D；

（2）若EB，求二面角D1﹣EC﹣D的大小．

Answer 1

【答案】（1）见解析（2）30°．

【解析】

（1）以D为原点，DA，DC，DD1所在直线分别为x，y，z轴，建立空间直角坐标系，

设AE＝t，（0≤t≤2），证明0即得证；（2）利用向量法求二面角D1﹣EC﹣D的大小．

证明：（1）以D为原点，DA，DC，DD1所在直线分别为x，y，z轴，建立空间直角坐标系，

设AE＝t，（0≤t≤2），则D1（0，0，1），E（1，t，0），A1（1，0，1），D（0，0，0），

（1，t，﹣1），（﹣1，0，﹣1），

所以0，

∴D1E⊥A1D．

（2）∵EB，∴E（1，2，0），C（0，2，0），

（1，，0），（0，﹣2，1），

设平面CED1的法向量（x，y，z），

则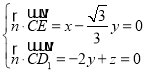，取y＝3，得（，6），

平面CDE的法向量（0，0，1），

设二面角D1﹣EC﹣D的平面角为θ，

则cosθ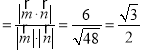，所以θ＝30°，

∴二面角D1﹣EC﹣D的大小为30°．