题目内容
设a∈R,f(x)为奇函数,f(2x)=| a•4x+a-2 | 4x+1 |
(1)写出函数f(x)的定义域;
(2)求a,并写出f(x)的表达式;
(3)用函数单调性定义证明:函数f(x)在定义域上是增函数.(可能用到的知识:若x1<x2,则0<2x1<2x2,0<4x1<4x2)
分析:(1)先用换元法由f(2x)求得f(x),再求f(x)的定义域.
(2)由f(x)为奇函数,得到f(-x)=-f(x)成立,用待定系数法求解.
(3)要求用定义证明,首先任意在定义域上任取两个变量,且界定其大小,再作差变形看符号,若自变量与函数值变化一致,则为增函数;若自变量与函数值变化相反,则为减函数.
(2)由f(x)为奇函数,得到f(-x)=-f(x)成立,用待定系数法求解.
(3)要求用定义证明,首先任意在定义域上任取两个变量,且界定其大小,再作差变形看符号,若自变量与函数值变化一致,则为增函数;若自变量与函数值变化相反,则为减函数.
解答:解:(1)由题意f(2x)=
∴f(x)=
(2分)
故函数f(x)的定义域为R(4分)
(2)∵f(x)为奇函数∴f(-x)=-f(x)对任意的x∈R都成立∴f(0)=0(7分)
即a+a-2=0∴a=1(10分)
所以f(x)=
=1-
(11分)
(3)对任意的x1,x2∈R且x1<x2(14分)f(x1)-f(x2)=1-
-(1-
)
=
-
=
<0(16分)
即f(x1)<f(x2)
函数f(x)在R上单调递增(17分)
| a22x+a-2 |
| 22x+1 |
| a2x+a-2 |
| 2x+1 |
故函数f(x)的定义域为R(4分)
(2)∵f(x)为奇函数∴f(-x)=-f(x)对任意的x∈R都成立∴f(0)=0(7分)
即a+a-2=0∴a=1(10分)
所以f(x)=
| 2x-1 |
| 2x+1 |
| 2 |
| 2x+1 |
(3)对任意的x1,x2∈R且x1<x2(14分)f(x1)-f(x2)=1-
| 2 |
| 2x1+1 |
| 2 |
| 2x2+1 |
=
| 2 |
| 2x2+1 |
| 2 |
| 2x1+1 |
=
| 2(2x1-2x2) |
| (2x1+1)(2x2+1) |
即f(x1)<f(x2)
函数f(x)在R上单调递增(17分)
点评:本题考查了换元法求函数解板式,求函数的定义域,奇偶性和单调性的应用,是函数性质考查中常见类型,要求熟练准确.

练习册系列答案
相关题目
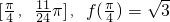 .给出下列几个命题:
.给出下列几个命题: 处取得小值;
处取得小值;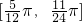 是f(x)的一个单调递减区间;
是f(x)的一个单调递减区间; .
.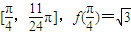 .给出下列几个命题:
.给出下列几个命题: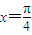 处取得小值;
处取得小值;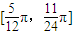 是f(x)的一个单调递减区间;
是f(x)的一个单调递减区间;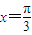 .
.