题目内容
设a∈R,f(x)=cosx(asinx-cosx)+sin2x的定义域是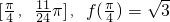 .给出下列几个命题:
.给出下列几个命题:
①f(x)在 处取得小值;
处取得小值;
②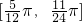 是f(x)的一个单调递减区间;
是f(x)的一个单调递减区间;
③f(x)的最大值为2;
④使得f(x)取得最大值的点仅有一个 .
.
其中正确命题的序号是________.(将你认为正确命题的序号都填上)
②③④
分析:利用二倍角公式化简函数f(x),然后由f( )=
)= ,求出a的值,进一步化简为f(x)=2sin(2x-
,求出a的值,进一步化简为f(x)=2sin(2x- ),然后根据x的范围求出2x-
),然后根据x的范围求出2x- 的范围,利用单调性求出函数的最大值和最小值.根据函数单调性及最值即可选出答案.
的范围,利用单调性求出函数的最大值和最小值.根据函数单调性及最值即可选出答案.
解答:f(x)=cosx(asinx-cosx)+sin2x=asinxcosx-cos2x+sin2x= sin2x-cos2x,
sin2x-cos2x,
由f( )=
)= ,得
,得 =
= ,解得a=2
,解得a=2 .
.
所以f(x)=2sin(2x- ),
),
当x∈[ ,
, ]时,2x-
]时,2x- ∈[
∈[ ,
, ],f(x)是增函数,
],f(x)是增函数,
当x∈[ ,
,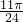 ]时,2x-
]时,2x- ∈[
∈[ ,
, ],f(x)是减函数,
],f(x)是减函数,
所以函数f(x)在[ ,
,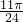 ]上的最大值是:f(
]上的最大值是:f( )=2,
)=2,
故③正确;
且当f(x)取得最大值的点仅有一个 .
.
故④正确;
由上述单调性知: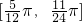 是f(x)的一个单调递减区间,
是f(x)的一个单调递减区间,
故②正确;
又f( )=
)= ,f(
,f(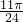 )=
)= ,
,
所以函数f(x)在[ ,
,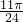 ]上的最小值为:f(
]上的最小值为:f(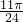 )=
)= ;
;
故①错误.
故答案为:②③④.
点评:本题是中档题,考查三角函数的化简,二倍角公式的应用,三角函数的求值,函数的单调性、最值,考查计算能力,常考题型.
分析:利用二倍角公式化简函数f(x),然后由f(
 )=
)= ,求出a的值,进一步化简为f(x)=2sin(2x-
,求出a的值,进一步化简为f(x)=2sin(2x- ),然后根据x的范围求出2x-
),然后根据x的范围求出2x- 的范围,利用单调性求出函数的最大值和最小值.根据函数单调性及最值即可选出答案.
的范围,利用单调性求出函数的最大值和最小值.根据函数单调性及最值即可选出答案.解答:f(x)=cosx(asinx-cosx)+sin2x=asinxcosx-cos2x+sin2x=
 sin2x-cos2x,
sin2x-cos2x,由f(
 )=
)= ,得
,得 =
= ,解得a=2
,解得a=2 .
.所以f(x)=2sin(2x-
 ),
),当x∈[
 ,
, ]时,2x-
]时,2x- ∈[
∈[ ,
, ],f(x)是增函数,
],f(x)是增函数,当x∈[
 ,
,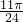 ]时,2x-
]时,2x- ∈[
∈[ ,
, ],f(x)是减函数,
],f(x)是减函数,所以函数f(x)在[
 ,
,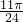 ]上的最大值是:f(
]上的最大值是:f( )=2,
)=2,故③正确;
且当f(x)取得最大值的点仅有一个
 .
.故④正确;
由上述单调性知:
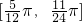 是f(x)的一个单调递减区间,
是f(x)的一个单调递减区间,故②正确;
又f(
 )=
)= ,f(
,f(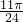 )=
)= ,
,所以函数f(x)在[
 ,
,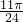 ]上的最小值为:f(
]上的最小值为:f(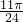 )=
)= ;
;故①错误.
故答案为:②③④.
点评:本题是中档题,考查三角函数的化简,二倍角公式的应用,三角函数的求值,函数的单调性、最值,考查计算能力,常考题型.

练习册系列答案
相关题目