题目内容
平面内给定三个向量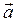 =(3,2),
=(3,2),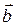 =(-1,2)
=(-1,2)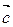 =(4,1).
=(4,1).
①若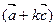 ∥
∥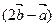 ,求实数k;
,求实数k;
②设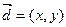 ,满足
,满足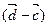 ⊥(
⊥(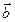 +
+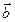 ),且
),且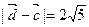 ,求
,求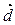
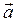 =(3,2),
=(3,2),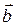 =(-1,2)
=(-1,2)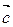 =(4,1).
=(4,1).①若
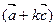 ∥
∥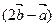 ,求实数k;
,求实数k;②设
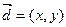 ,满足
,满足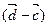 ⊥(
⊥(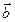 +
+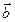 ),且
),且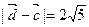 ,求
,求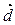
(1) (2)
(2)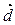 =(8,-1)或
=(8,-1)或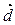 =(0,3)
=(0,3)
 (2)
(2)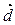 =(8,-1)或
=(8,-1)或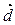 =(0,3)
=(0,3)① =(3 + 4k,2 + k),
=(3 + 4k,2 + k), =(-5,2),
=(-5,2),
 ∴2(3 + 4k)+5(2 + k)= 0,解得
∴2(3 + 4k)+5(2 + k)= 0,解得 .
.
② =" (" x – 4,y -1),
=" (" x – 4,y -1),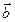 +
+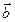 =(2,4),∴
=(2,4),∴
解得 或 ∴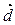 =(8,-1)或
=(8,-1)或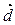 =(0,3)
=(0,3)
 =(3 + 4k,2 + k),
=(3 + 4k,2 + k), =(-5,2),
=(-5,2), ∴2(3 + 4k)+5(2 + k)= 0,解得
∴2(3 + 4k)+5(2 + k)= 0,解得 .
. ②
 =" (" x – 4,y -1),
=" (" x – 4,y -1),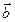 +
+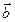 =(2,4),∴
=(2,4),∴  |  |
解得 或 ∴
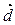 =(8,-1)或
=(8,-1)或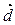 =(0,3)
=(0,3) 
练习册系列答案
相关题目
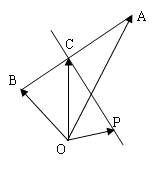
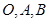 是平面上的三点,向量
是平面上的三点,向量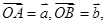 点C是线段AB的中点,设
点C是线段AB的中点,设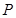 为线段
为线段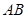 的垂直平分线
的垂直平分线 上任意一点,向量
上任意一点,向量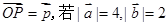 ,则
,则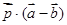 = ▲ .
= ▲ .
 ,
, .
. 与
与 共线时,求
共线时,求 的值;
的值;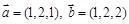 ,且
,且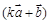 ∥
∥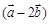 ,则实数
,则实数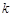 的值为 .
的值为 .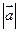 =
=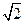
 =2,且(
=2,且(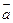 -
-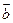 )
)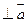 ,则
,则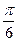
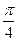
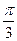
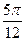
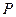 的斜坐标定义为:若
的斜坐标定义为:若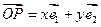 (其中
(其中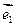 、
、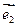 分别为斜坐标系的
分别为斜坐标系的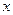 轴、
轴、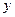 轴正方向上的单位向量,
轴正方向上的单位向量,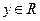 ),则点
),则点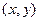 .在平面斜坐标系
.在平面斜坐标系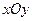 中,若
中,若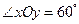 ,已知点
,已知点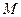 的斜坐标为
的斜坐标为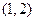 ,则点
,则点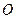 的距离为 .
的距离为 .