题目内容
【题目】设函数f（x）=kx2﹣kx，g（x）= 
，若使得不等式f（x）≥g（x）对一切正实数x恒成立的实数k存在且唯一，则实数a的值为 ．
【答案】2
【解析】解：由题意：函数f（x）=，g（x）= 
，
当g（x）=lnx（x≥1），图象过（1，0），使得不等式f（x）≥g（x）对一切正实数x恒成立的实数k存在且唯一，即kx2﹣kx﹣lnx≥0，令m（x）=kx2﹣kx﹣lnx≥0
则m′（x）=2kx﹣k﹣ 
≥0．
实数k存在且唯一，当x=1时，解得k=1．
即k=1．可得函数f（x）=x2﹣x．
当0＜x＜1时，要使f（x）≥g（x）对一切正实数x恒成立，即x2﹣x≥﹣x3+（a+1）x2﹣ax．
令h（x）=x2﹣ax+a﹣1≥0，
∵对一切正实数x恒成立且唯一，
∴△=a2﹣4（a﹣1）=0，
解得：a=2．
所以答案是：2．
阅读快车系列答案
【题目】函数f（x）=6cos2 
+ 
sinωx﹣3（ω＞2）在一个周期内的图象如图所示，A为图象的最高点，B，C为图象与x轴的交点，且ABC为正三角形．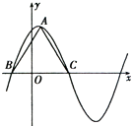 
（1）求ω的值；
（2）求函数f（x）的值域．
【题目】为了了解甲、乙两所学校全体高三年级学生在该地区八校联考中的数学成绩情况，从两校各随机抽取60名学生，将所得样本作出频数分布统计表如下： 甲校：
分组 | [70，80） | [80，90） | [90，100） | [100，110） |
频数 | 2 | 5 | 9 | 10 |
分组 | [110，120） | [120，130） | [130，140） | [140，150] |
频数 | 14 | 10 | 6 | 4 |
乙校：
分组 | [70，80） | [80，90） | [90，100） | [100，110） |
频数 | 2 | 4 | 8 | 16 |
分组 | [110，120） | [120，130） | [130，140） | [140，150] |
频数 | 15 | 6 | 6 | 3 |
以抽样所得样本数据估计总体
（1）比较甲、乙两校学生的数学平均成绩的高低；
（2）若规定数学成绩不低于120分为优秀，从甲、乙两校全体高三学生中各随机抽取2人，其中数学成绩为优秀的共X人，求X的分布列及数学期望．
