题目内容
16.求满足下列条件的直线方程:(1)经过点(-2,3),且与直线2x-3y-7=0平行;
(2)经过点(3,1),且与直线x-2y-2=0垂直;
(3)经过点(0,-2)及直线2x-y-2=0与x-3y-7=0.
分析 (1)设与直线2x-3y-7=0平行的直线方程为2x-3y+m=0;把点(-2,3)代入解得m即可得出.
(2)设与直线x-2y-2=0垂直的直线方程为2x+y+n=0;把点(3,1)代入解得n即可得出.
(3)联立$\left\{\begin{array}{l}{2x-y-2=0}\\{x-3y-7=0}\end{array}\right.$,解得交点P$(-\frac{1}{5},-\frac{12}{5})$.求出斜率k,利用点斜式即可得出.
解答 解:(1)设与直线2x-3y-7=0平行的直线方程为2x-3y+m=0;
把点(-2,3)代入可得:-4-9+m=0,解得m=13.
∴要求的直线方程为2x-3y+13=0.
(2)设与直线x-2y-2=0垂直的直线方程为2x+y+n=0;
把点(3,1)代入可得:6+1+n=0,解得n=-7.
∴要求的直线方程为2x+y-7=0.
(3)联立$\left\{\begin{array}{l}{2x-y-2=0}\\{x-3y-7=0}\end{array}\right.$,解得交点P$(-\frac{1}{5},-\frac{12}{5})$.
∴k=$\frac{-2+\frac{12}{5}}{0+\frac{1}{5}}$=2,
∴要求的直线方程为:y+2=2x,即2x-y-2=0.
点评 本题考查了相互平行及其垂直的直线斜率之间的关系、点斜式方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知双曲线M:9x2-16y2=144,若椭圆N以M的焦点为顶点,以M的顶点为焦点,则椭圆N的准线方程是( )
| A. | x=±$\frac{16}{5}$ | B. | x=±$\frac{25}{4}$ | C. | x=±$\frac{16}{3}$ | D. | x=±$\frac{25}{3}$ |
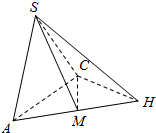 如图在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=$\sqrt{2}$,M为AB的中点.
如图在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=$\sqrt{2}$,M为AB的中点.