题目内容
11.在△ABC中,角A、B、C所对的边分别为a,b,c,且满足 2acosC=2b-c.(1)求sinA的值;
(2)若a=1,求△ABC的周长l的取值范围.
分析 (1)由题意和正弦定理以及和差角的三角函数公式可得cosA=$\frac{1}{2}$,进而可得sinA=$\frac{\sqrt{3}}{2}$;
(2)由(1)可得a=1,sinA=$\frac{\sqrt{3}}{2}$,A=$\frac{π}{3}$,结合正弦定理可得l=1+$\frac{2}{\sqrt{3}}$sinB+$\frac{2}{\sqrt{3}}$sinC=1+2sin(B+$\frac{π}{6}$),由B∈(0,$\frac{2π}{3}$)和三角函数的值域可得.
解答 解:(1)由题意可得2acosC=2b-c,
结合正弦定理可得 2sinAcosC=2sinB-sinC,
∴2sinAcosC=2sin(A+C)-sinC,
∴2sinAcosC=2sinAcosC+2cosAsinC-sinC,
∴2cosAsinC=sinC,即cosA=$\frac{1}{2}$,
∴sinA=$\frac{\sqrt{3}}{2}$;
(2)由(1)可得a=1,sinA=$\frac{\sqrt{3}}{2}$,A=$\frac{π}{3}$,
∴b=$\frac{asinB}{sinA}$=$\frac{2}{\sqrt{3}}$sinB,同理可得c=$\frac{2}{\sqrt{3}}$sinC,
∴△ABC的周长l=1+$\frac{2}{\sqrt{3}}$sinB+$\frac{2}{\sqrt{3}}$sinC
=1+$\frac{2}{\sqrt{3}}$sinB+$\frac{2}{\sqrt{3}}$sin($\frac{2π}{3}$-B)
=1+$\frac{2}{\sqrt{3}}$(sinB+$\frac{\sqrt{3}}{2}$cosB+$\frac{1}{2}$sinB)
=1+$\frac{2}{\sqrt{3}}$($\frac{3}{2}$sinB+$\frac{\sqrt{3}}{2}$cosB)
=1+2sin(B+$\frac{π}{6}$),
∴B∈(0,$\frac{2π}{3}$),∴B+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{5π}{6}$),
∴sin(B+$\frac{π}{6}$)∈($\frac{1}{2}$,1],
∴2sin(B+$\frac{π}{6}$)∈(1,2],
∴1+2sin(B+$\frac{π}{6}$)∈(2,3],
∴△ABC的周长l的取值范围为(2,3].
点评 本题考查解三角形,涉及正余弦定理和和差角的三角函数,属中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | y=x+1 | B. | y=$\frac{1}{x}$ | C. | y=x4 | D. | y=x5 |
| A. | I>1 | B. | I<1 | C. | I=1 | D. | 以上都不对 |
| A. | $\frac{15}{4}$ | B. | $\frac{17}{4}$ | C. | $\frac{1}{2}ln2$ | D. | 2ln2 |
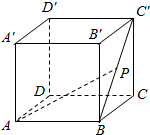 如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.
如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.