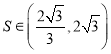题目内容
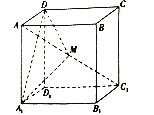
【题目】某企业拥有3条相同的生产线,每条生产线每月至多出现一次故障.各条生产线是否出现故障相互独立,且出现故障的概率为![]() .
.
(1)求该企业每月有且只有1条生产线出现故障的概率;
(2)为提高生产效益,该企业决定招聘名维修工人及时对出现故障的生产线进行维修.已知每名维修工人每月只有及时维修1条生产线的能力,且每月固定工资为1万元.此外,统计表明,每月在不出故障的情况下,每条生产线创造12万元的利润;如果出现故障能及时维修,每条生产线创造8万元的利润;如果出现故障不能及时维修,该生产线将不创造利润,以该企业每月实际获利的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
【答案】(1)![]() (2)应选用
(2)应选用![]()
【解析】
(1)分析可得随机变量满足二项分布,求得![]() 时的概率即可;
时的概率即可;
(2)由(1),并分别求得![]() ,
,![]() ,
,![]() 时的概率,由题意得到不同方案下实际获利并求得期望,比较大小即可
时的概率,由题意得到不同方案下实际获利并求得期望,比较大小即可
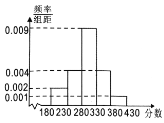
解:(1)设3条生产线中出现故障的条数为![]() ,则
,则![]() ,
,
因此
(2)①当![]() 时,设该企业每月的实际获利为
时,设该企业每月的实际获利为![]() 万元,
万元,
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ;
;
又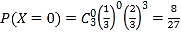 ,
, ,
,
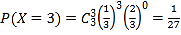 ,
,
此时,实际获利![]() 的均值
的均值![]()
②当![]() 时,设该企业每月的实际获利为
时,设该企业每月的实际获利为![]() 万元,
万元,
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ;
;
![]()
因为![]() ,
,
于是以该企业每月实际获利的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用
之中选其一,应选用![]()

 阶梯计算系列答案
阶梯计算系列答案【题目】某饼屋进行为期![]() 天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满
天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满![]() 元,可得
元,可得![]() 元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了
元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了![]() 位顾客一次性消费的金额数(元),频数分布表如下图所示:
位顾客一次性消费的金额数(元),频数分布表如下图所示:
一次性消费金额数 |
|
|
|
|
|
人数 |
|
|
|
|
|
以这![]() 位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
(1)预计该店每天的客流量为![]() 人次,求这次店庆期间,商家每天送出代金券金额数的期望;
人次,求这次店庆期间,商家每天送出代金券金额数的期望;
(2)假设顾客获得一元或两元红包的可能性相等,商家在店庆活动结束后会公布幸运数字,连续![]() 天参加返红包的顾客,如果红包金额总数与幸运数字一致,则可再获得
天参加返红包的顾客,如果红包金额总数与幸运数字一致,则可再获得![]() 元的“店庆幸运红包”一个.若公布的幸运数字是“
元的“店庆幸运红包”一个.若公布的幸运数字是“![]() ”,求店庆期间一位连续
”,求店庆期间一位连续![]() 天消费的顾客获得红包金额总数的期望.
天消费的顾客获得红包金额总数的期望.
【题目】人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间![]() 内的一个数来表示,该数越接近
内的一个数来表示,该数越接近![]() 表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各
表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各![]() 人进行了调查,调查数据如表所示:
人进行了调查,调查数据如表所示:
幸福感指数 |
|
|
|
|
|
男居民人数 |
|
|
|
|
|
女居民人数 |
|
|
|
|
|
(1)估算该地区居民幸福感指数的平均值;
(2)若居民幸福感指数不小于![]() ,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取
,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取![]() 对夫妻进行调查,用
对夫妻进行调查,用![]() 表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求
表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求![]() 的期望(以样本的频率作为总体的概率).
的期望(以样本的频率作为总体的概率).