题目内容
已知双曲线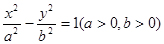 的渐近线与圆
的渐近线与圆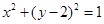 相切,则双曲线的离心率为( )
相切,则双曲线的离心率为( )
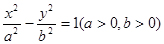 的渐近线与圆
的渐近线与圆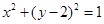 相切,则双曲线的离心率为( )
相切,则双曲线的离心率为( )A. | B.2 | C.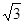 | D.3 |
B
试题分析:根据题意,由于双曲线
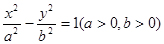 的渐近线与圆
的渐近线与圆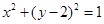 相切,那么可知圆心(0,2)到直线
相切,那么可知圆心(0,2)到直线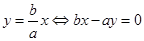 的距离为圆的半径为1,即可知
的距离为圆的半径为1,即可知 ,则其离心率为
,则其离心率为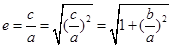 =2,故答案为B.
=2,故答案为B.点评:本题以双曲线方程与圆的方程为载体,考查直线与圆相切,考查双曲线的几何性质,解题的关键是利用直线与圆相切时,圆心到直线的距离等于半径

练习册系列答案
相关题目
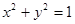 过椭圆
过椭圆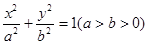 的两焦点,与椭圆有且仅有两个公共点:直线
的两焦点,与椭圆有且仅有两个公共点:直线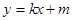 与圆
与圆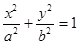 相交于A,B两点记
相交于A,B两点记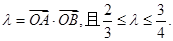
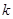 的取值范围;
的取值范围;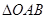 的面积S的取值范围.
的面积S的取值范围.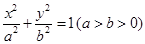 的左焦点为
的左焦点为 ,过点
,过点 ,
, 两点.当直线
两点.当直线 经过椭圆的一个顶点时,其倾斜角恰为
经过椭圆的一个顶点时,其倾斜角恰为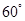 .
.
 ,
,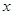 轴和
轴和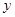 轴分别交于
轴分别交于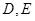 两点,
两点,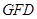 的面积为
的面积为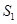 ,△
,△ (
(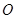 为原点)的面积为
为原点)的面积为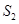 ,求
,求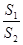 的取值范围.
的取值范围.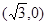
 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且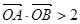 (其中O为原点). 求k的取值范围.
(其中O为原点). 求k的取值范围.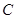 的极坐标方程为
的极坐标方程为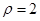 ,以极点为直角坐标系的原点,极轴为
,以极点为直角坐标系的原点,极轴为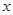 轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆
轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆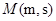 作平行于
作平行于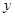 轴的直线
轴的直线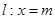 ,设
,设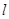 与
与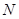 ,向量
,向量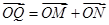 .
.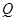 的轨迹方程;
的轨迹方程;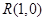 ,求
,求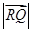 的最小值.
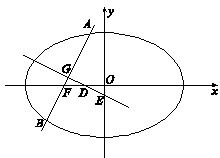
的最小值.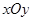 中,点
中,点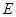 到两点
到两点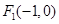 ,
,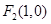 的距离之和为
的距离之和为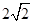 ,设点
,设点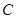 .
.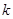 (
(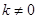 )的直线
)的直线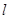 与曲线
与曲线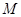 ,
,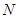 ,点
,点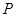 在
在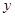 轴上,且
轴上,且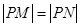 ,求点
,求点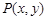 在椭圆
在椭圆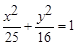 上,若
上,若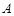 点坐标为
点坐标为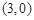 ,
,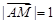 ,且
,且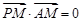 ,则
,则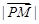 的最小值是( )
的最小值是( )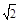
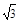

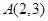 关于直线
关于直线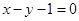 的对称点
的对称点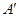 的坐标为 ;
的坐标为 ;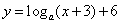 (
(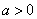 ,
,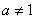 )的图象恒过定点
)的图象恒过定点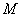 ,椭圆
,椭圆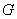 :
: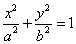 (
(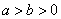 )的左,右焦点分别为
)的左,右焦点分别为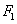 ,
,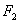 ,直线
,直线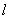 经过点
经过点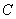 :
: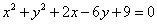 相切.
相切.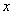 轴上方的交点为
轴上方的交点为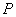 ,且
,且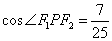 ,求
,求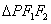 内切圆的方程.
内切圆的方程.