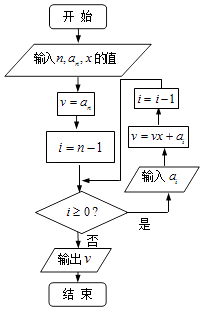
题目内容
【题目】已知双曲线C1: ![]() =1,双曲线C2:
=1,双曲线C2: ![]() =1(a>0,b>0)的左、右焦点分别为F1 , F2 , M 是双曲线C2 一条渐近线上的点,且OM⊥MF2 , 若△OMF2的面积为 16,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长为( )
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , M 是双曲线C2 一条渐近线上的点,且OM⊥MF2 , 若△OMF2的面积为 16,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长为( )
A.4
B.8
C.16
D.32
【答案】C
【解析】解:双曲线C1: ![]() =1的离心率为e=
=1的离心率为e= ![]() =
= ![]() =
= ![]() =
= ![]() , 设F2(c,0),双曲线C2一条渐近线方程为y=
, 设F2(c,0),双曲线C2一条渐近线方程为y= ![]() x,
x,
可得|F2M|= ![]() =
= ![]() =b,
=b,
即有|OM|= ![]() =a,
=a,
由△OMF2的面积为16,可得 ![]() ab=16,
ab=16,
即ab=32,又a2+b2=c2 , 且 ![]() =
= ![]() ,
,
解得a=8,b=4,c=4 ![]() ,
,
即有双曲线的实轴长为16.
故选:C.
求得双曲线C1的离心率,求得双曲线C2一条渐近线方程为y= ![]() x,运用点到直线的距离公式,结合勾股定理和三角形的面积公式,化简整理解方程可得a=8,进而得到双曲线的实轴长.
x,运用点到直线的距离公式,结合勾股定理和三角形的面积公式,化简整理解方程可得a=8,进而得到双曲线的实轴长.

练习册系列答案
相关题目