题目内容
如图,已知三棱锥A—BPC中,AP⊥PC, AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形。
(Ⅰ)求证:DM∥平面APC;
(Ⅱ)求证:平面ABC⊥平面APC;
(Ⅲ)若BC=4,AB=20,求三棱锥D—BCM的体积.
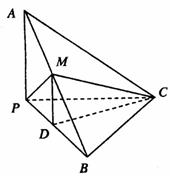
解:(Ⅰ)由已知得,![]() 是
是![]() ABP的中位线
ABP的中位线
![]()
![]() ……………2分
……………2分
![]()
![]()
![]() ……………4分
……………4分

(Ⅱ)![]() 为正三角形,D为PB的中点,
为正三角形,D为PB的中点,
![]()
![]() , …………………5分
, …………………5分
![]()
![]() …………………6分
…………………6分
又![]()
![]()
![]() ……………………7分
……………………7分
![]()
![]()
![]()
又![]()
![]() ………………9分
………………9分
![]()
![]() 平面ABC⊥平面APC ………………10分
平面ABC⊥平面APC ………………10分
(Ⅲ)∵![]() ,
,![]()
![]() 是三棱锥M—DBC的高,且MD=
是三棱锥M—DBC的高,且MD=![]() …11分
…11分
又在直角三角形PCB中,由PB=10,BC=4,可得PC=![]() ………12分
………12分
于是![]() =
=![]() , ………………………………………………13分
, ………………………………………………13分
![]()
![]() =
=![]() …………………………14分
…………………………14分

练习册系列答案
相关题目
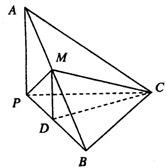 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.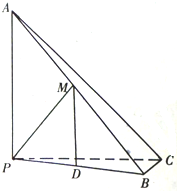 如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP.
如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP.
 如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )
如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( ) 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.