题目内容
 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.(1)求证:DM∥平面APC;
(2)若BC=4,AB=20,求三棱锥D-BCM的体积.
分析:(1)可由三角形的中位线定理得到线线平行,进而得到线面平行.
(2)先证明MD⊥底面BCD,进而可计算出体积.
(2)先证明MD⊥底面BCD,进而可计算出体积.
解答:(1)证明:∵M为AB的中点,D为PB的中点,∴MD为△PAB的中位线,∴MD∥AP.
而AP?平面PAC,MD?平面PAC,
∴MD∥平面PAC.
(2)解:∵△PMB为正三角形,PD=DB,∴MD⊥PB.
∵MD∥AP,AP⊥PC,∴MD⊥PC.
又PC∩PB=P,∴MD⊥平面PBC.即MD为三棱锥M-BCD的高.
由AB=20,∴MB=10,BD=5,∴MD=5
.
在Rt△PCB中,由勾股定理得PC=
=2
.
于是S△BCD=S△BCP×
=
×
×2
×4=2
.
∴V三棱锥D-BCM=V三棱锥M-BCD=
×2
×5
=10
.
而AP?平面PAC,MD?平面PAC,
∴MD∥平面PAC.
(2)解:∵△PMB为正三角形,PD=DB,∴MD⊥PB.
∵MD∥AP,AP⊥PC,∴MD⊥PC.
又PC∩PB=P,∴MD⊥平面PBC.即MD为三棱锥M-BCD的高.
由AB=20,∴MB=10,BD=5,∴MD=5
| 3 |
在Rt△PCB中,由勾股定理得PC=
| 102-42 |
| 21 |
于是S△BCD=S△BCP×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 21 |
| 21 |
∴V三棱锥D-BCM=V三棱锥M-BCD=
| 1 |
| 3 |
| 21 |
| 3 |
| 7 |
点评:利用三角形的中位线定理证明线线平行是证明线面平行常用的方法之一.先证明线面垂直是求体积的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
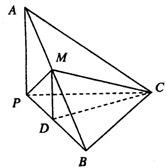 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.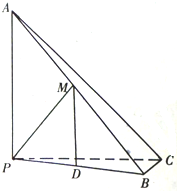 如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP.
如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP.
 如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )
如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )