题目内容
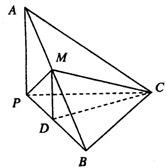 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.
分析:(1)要证DM∥平面APC,只需证明MD∥AP(因为AP?面APC)即可.
(2)在平面ABC内直线AP⊥BC,BC⊥AC,即可证明BC⊥面APC,从而证得平面ABC⊥平面APC;
(3)因为BC=4,AB=20,求出三棱锥的高,即可求三棱锥D-BCM的体积.
(2)在平面ABC内直线AP⊥BC,BC⊥AC,即可证明BC⊥面APC,从而证得平面ABC⊥平面APC;
(3)因为BC=4,AB=20,求出三棱锥的高,即可求三棱锥D-BCM的体积.
解答:证明:(I)由已知得,MD是△ABP的中位线
∴MD∥AP∵MD?面APC,AP?面APC
∴MD∥面APC;(4分)
(II)∵△PMB为正三角形,D为PB的中点
∴MD⊥PB,∴AP⊥PB又∵AP⊥PC,PB∩PC=P
∴AP⊥面PBC(6分)∵BC?面PBC∴AP⊥BC
又∵BC⊥AC,AC∩AP=A∴BC⊥面APC,(8分)
∵BC?面ABC∴平面ABC⊥平面APC;(10分)
(III)由题意可知,MD⊥面PBC,
∴MD是三棱锥D-BCM的高,
∴VM-DBC=
Sh=10
.(14分)
∴MD∥AP∵MD?面APC,AP?面APC
∴MD∥面APC;(4分)
(II)∵△PMB为正三角形,D为PB的中点
∴MD⊥PB,∴AP⊥PB又∵AP⊥PC,PB∩PC=P
∴AP⊥面PBC(6分)∵BC?面PBC∴AP⊥BC
又∵BC⊥AC,AC∩AP=A∴BC⊥面APC,(8分)
∵BC?面ABC∴平面ABC⊥平面APC;(10分)
(III)由题意可知,MD⊥面PBC,
∴MD是三棱锥D-BCM的高,
∴VM-DBC=
| 1 |
| 3 |
| 7 |
点评:本题考查直线与平面的平行,三棱锥的体积,平面与平面垂直的判定,是中档题.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
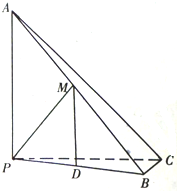 如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP.
如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP.
 如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )
如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( ) 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.