题目内容
13.某企业投资1千万元于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金100万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过n年后该项目的资金为an万元.(1)写出数列{an}的前三项a1,a2,a3,并猜想写出通项an.
(2)求经过多少年后,该项目的资金可以达到或超过2千万元.
分析 (1)利用已知条件写出数列{an}的前三项a1,a2,a3,然后猜想通项an.
(2)该项目的资金可以达到或超过2千万元.通过an≥2000,得到不等式求解即可.
解答 解:(1)依题意${a_1}={10^3}×\frac{5}{4}-100,{a_2}={a_1}×\frac{5}{4}-100={10^3}×{({\frac{5}{4}})^2}-100×({1+\frac{5}{4}})$${a_3}={a_2}×\frac{5}{4}-100={10^3}×{({\frac{5}{4}})^3}-100×[{1+\frac{5}{4}+{{({\frac{5}{4}})}^2}}]$
猜想${a_n}={10^3}×{({\frac{5}{4}})^n}-100×[{1+\frac{5}{4}+{{({\frac{5}{4}})}^2}+…+{{({\frac{5}{4}})}^{n-1}}}]$
=${10^3}×{({\frac{5}{4}})^n}-100×\frac{{1-{{({\frac{5}{4}})}^n}}}{{1-\frac{5}{4}}}=600×{({\frac{5}{4}})^n}+400$
(2)由an≥2000,得$600×{({\frac{5}{4}})^n}+400≥2000$∴${({\frac{5}{4}})^n}≥\frac{8}{3}$
∵$y={({\frac{5}{4}})^x}$在(-∞,+∞)上单调递增,估算 ${({\frac{5}{4}})^4}<\frac{8}{3}$,${({\frac{5}{4}})^5}>\frac{8}{3}$∴n≥5
答:要经过5年,该项目的资金超过2千万元.
点评 本题考查数列的应用,数列与函数相结合,考查计算能力.

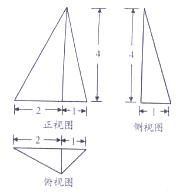 若某几何体的三视图如图所示,则该几何体的体积为( )
若某几何体的三视图如图所示,则该几何体的体积为( )| A. | 1 | B. | $\frac{4}{3}$ | C. | 2 | D. | 6 |
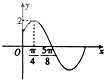 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.