Question

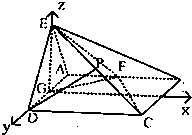
如图，平面EAD⊥平面ABCD，△ADE是等边三角形，ABCD是矩形，AD=2，AB=2

2

，F、G分别是AB、AD的中点．
（1）求证：CF⊥平面EFG；
（2）若P为线段CE上一点，且

CP

=

1

3

CE

，求DP与平面EFG所成的角．

Answer 1

考点：直线与平面所成的角,直线与平面垂直的判定

专题：空间向量及应用

分析：（1）根据线面垂直的判定定理即可证明CF⊥平面EFG；
（2）建立坐标系，即可DP与平面EFG所成的角．

解答： 解：（1）∵平面EAD⊥平面ABCD，EG⊥AD，
∴EG⊥平面ABCD，且EG=

3

以GE为z轴、AD为y轴建立如图所示
空间直角坐标系，
则E（0，0，

3

），D（0，1，0），
C（2

2

，1，0），F（

2

，-1，0）．

GF

=(

2

，-1，0)，

EF

=(

2

，-1，-

3

)，

FC

=(

2

，2，0)．
∴

GF

•

FC

=0，

EF

•

FC

=0
∴CF⊥FG，CF⊥EF，则CF⊥平面EFG．
（2）∵

CP

=

1

3

CE

=

1

3

•(-2

2

，-1，

3

)=(-

2 2

3

，-

1

3

，

3

3

)=(2

2

，0，0)
∴

DP

=

DC

+

CP

=(

4 2

3

，-

1

3

，

3

3

)．
由（1）知=(

2

，2，0)为平面EFG的一个法向量，
∵

DP

•

FC

=2，|

FC

|=

6

，|

DP

|=2
∴cos(

DP

，

FC

)=

6

6

∴DP与平面EFG所成的角为arsin

6

6

．

点评：本题主要考查直线和平面所成角的求解，以及线面垂直的判定，利用向量法是解决本题的关键．