题目内容
17.已知动点P在棱长为1的正方体ABCD-A1B1C1D1的表面上运动,且PA=r(0<r<$\sqrt{3}$),记点P的轨迹长度为f(r)给出以下四个命题:①f(1)=$\frac{3}{2}$π
②f($\sqrt{2}$)=$\sqrt{3}$π
③f($\frac{2\sqrt{3}}{3}$)=$\frac{2\sqrt{3}}{3}$π
④函数f(r)在(0,1)上是增函数,f(r)在($\sqrt{2}$,$\sqrt{3}$)上是减函数
其中为真命题的是①④(写出所有真命题的序号)
分析 由题意画出图形并得出相应的解析式,画出其图象,经过讨论即可得出答案.
解答 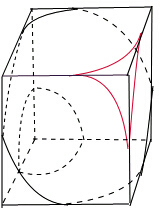 解:如图所示:①当0<r≤1时,f(r)=3×$\frac{π}{2}$×r=$\frac{3π}{2}$r,f($\frac{1}{2}$)=$\frac{3π}{4}$,
解:如图所示:①当0<r≤1时,f(r)=3×$\frac{π}{2}$×r=$\frac{3π}{2}$r,f($\frac{1}{2}$)=$\frac{3π}{4}$,
.此时,由一次函数的单调性可得:
0<f(r)≤$\frac{3π}{2}$<5,
②当1<r≤$\sqrt{2}$时,在平面ABCD内,设以点A为圆心,r为半径的圆弧与BC、CD分别交于点E、F,则
cos∠DAF=$\frac{1}{r}$,∠EAF=$\frac{π}{2}$-2∠DAF,
∴cos∠EAF=sin2∠DAF=2$\sqrt{1-(\frac{1}{r})^{2}}×\frac{1}{r}$=$\frac{2\sqrt{{r}^{2}-1}}{{r}^{2}}$,
cos∠EAG=$\frac{2{r}^{2}-(\sqrt{2}\sqrt{{r}^{2}-1})^{2}}{2{r}^{2}}=\frac{1}{{r}^{2}}$,
∴f(r)=3rarccos$\frac{2\sqrt{{r}^{2}-1}}{{r}^{2}}$+3rarccos$\frac{1}{{r}^{2}}$;
③当$\sqrt{2}$<r≤$\sqrt{3}$时,∵CM=$\sqrt{{r}^{2}-2}$,
∴${C}_{1}M={C}_{1}N=1-\sqrt{{r}^{2}-2}$,
∴cos∠MAN=$\frac{2{r}^{2}-[\sqrt{2}(1-\sqrt{{r}^{2}-2})]^{2}}{2{r}^{2}}$=$\frac{1+2\sqrt{{r}^{2}-2}}{{r}^{2}}$,
∴f(r)=3rarccos$\frac{1+2\sqrt{{r}^{2}-2}}{{r}^{2}}$,
综上,当0<r≤1时,f(r)=$\frac{3π}{2}$r,
当1<r≤$\sqrt{2}$时,f(r)=3rarccos$\frac{2\sqrt{{r}^{2}-1}}{{r}^{2}}$+3rarccos$\frac{1}{{r}^{2}}$;
当$\sqrt{2}$<r≤$\sqrt{3}$时,f(r)=3rarccos$\frac{1+2\sqrt{{r}^{2}-2}}{{r}^{2}}$,
故只有①④正确.
故答案为:①④.
点评 熟练掌握数形结合、分类讨论的思想方法、数形结合的思想方法是解题的关键.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |

| A. | 12 | B. | 8$\sqrt{3}$ | C. | 8 | D. | 6$\sqrt{3}$ |
| A. | 29 | B. | 28 | C. | 27 | D. | 26 |
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{10}$ |