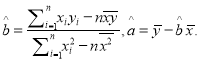题目内容
【题目】某幼儿园根据部分同年龄段的100名女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
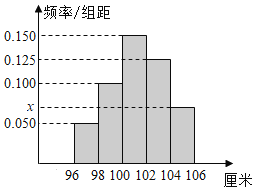
(1)求出![]() 的值,并求样本中女童的身高的众数和中位数,平均数;
的值,并求样本中女童的身高的众数和中位数,平均数;
(2)在身高在[100,102),[102,104),[104,106]的三组中,用分层抽样的方法抽取14名女童,则身高数据在[104,106]的女童中应抽取多少人数?
【答案】(1)![]() ;众数为
;众数为![]() ;中位数约为
;中位数约为![]() ;平均数为
;平均数为![]()
(2)![]()
【解析】
(1)根据小矩形的面积之和等于![]() 可求
可求![]() 的值;取高度最高的小矩形底边中点横坐标即为众数;设中位数为
的值;取高度最高的小矩形底边中点横坐标即为众数;设中位数为![]() ,由
,由![]() 即可求解;利用小矩形的面积与小矩形底边中点横坐标乘积的所有和即可求解.
即可求解;利用小矩形的面积与小矩形底边中点横坐标乘积的所有和即可求解.
(2)根据三组的比例关系即可求解.
(1)由![]() ,
,
解得![]() ,
,
由频率分布直方图可知,众数为![]() ,
,
设中位数为![]() ,则
,则![]() ,
,
解得![]() ,
,
平均数![]()
![]() .
.
(2)由频率分布直方图可知身高在[100,102),[102,104),[104,106]的比例为
![]() ,
,
所以分层抽样的方法抽取14名女童,
身高数据在[104,106]的女童中应抽取:![]()

 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
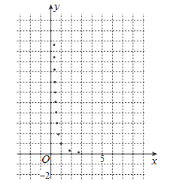
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为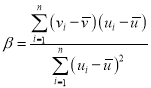 ,
,![]() .
.