题目内容
10.求数列$\frac{1}{1×3}$,$\frac{1}{3×5}$,$\frac{1}{5×7}$,…$\frac{1}{(2n-1)(2n+1)}$的前n项和.分析 直接利用裂项相消法求数列的前n项和.
解答 解:由$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
得数列$\frac{1}{1×3}$,$\frac{1}{3×5}$,$\frac{1}{5×7}$,…$\frac{1}{(2n-1)(2n+1)}$的前n项和为
${S}_{n}=\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$=$\frac{1}{2}(1-\frac{1}{2n+1})=\frac{n}{2n+1}$.
点评 本题考查了裂项相消法求数列的和,涉及等差数列连续两项乘积倒数构成的数列求和问题常采用裂项相消法,是中档题.

练习册系列答案
相关题目
6.正方体的棱长为1,C、D、M分别为三条棱的中点,A、B是顶点,那么点M到截面ABCD的距离是( ) 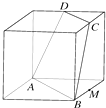

| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.