题目内容
设双曲线C：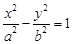
(a＞0，b＞0)的右焦点为F，左，右顶点分别为A1，A2．过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P，若P恰好在以A1A2为直径的圆上，则双曲线C的离心率为
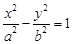(a＞0，b＞0)的右焦点为F，左，右顶点分别为A1，A2．过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P，若P恰好在以A1A2为直径的圆上，则双曲线C的离心率为A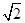． | B．2 | C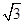． | D． 3 |
A
解：由题意可得：双曲线C：
的渐近线方程为：y=±
x，
所以设直线l的方程为：y= (x-c)，则直线l与双曲线的另一条渐近线的交点为：P（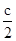
，-
），
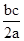所以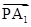
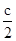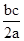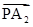=(-a-，)，
=(a-，)．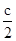
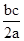因为P恰好在以A1A2为直径的圆上，
所以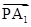?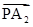=0，即(-a-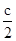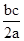，) ?(a-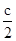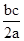，)=0，
所以整理可得：b2c2=4a4-a2c2
所以结合b2=c2-a2可得：2a2=c2，所以e=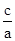
=
．
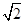故选A．
的渐近线方程为：y=±x，所以设直线l的方程为：y=
(x-c)，则直线l与双曲线的另一条渐近线的交点为：P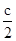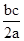（，-），所以
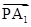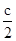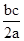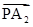=(-a-，)，=(a-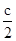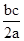，)．因为P恰好在以A1A2为直径的圆上，
所以
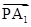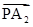?=0，即(-a-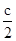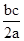，) ?(a-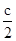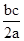，)=0，所以整理可得：b2c2=4a4-a2c2
所以结合b2=c2-a2可得：2a2=c2，所以e=
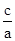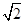=．故选A．
练习册系列答案
相关题目
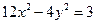有相同的焦点，且过点
.
、
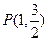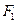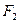是椭圆G的左焦点和右焦点，过
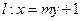与椭圆G相交于A、B两点，请问
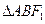的内切圆M的面积是否存在最大值？若存在,求出这个最大值及直线
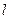的方程，若不存在,请说明理由.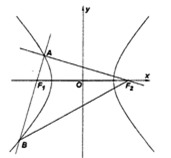
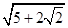
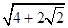
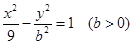的一个焦点坐标是
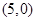，则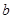
等于（ ）.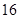
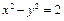绕原点逆时针旋转
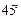后可得到双曲线
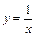．据此类推可求得双曲线
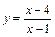的焦距为
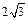
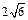
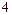
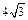
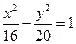上一点，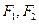
分别是双曲线左右两个焦点，若
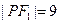，则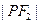
=（ ）
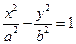的渐近线与抛物线
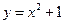有且只有两个公共点，则该双曲线的离心率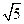
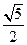
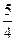
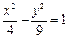的渐近线方程是 ( )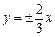
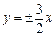
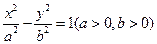的左、右焦点分别是
、
，过点
、
．若△
为正三角形，则该双曲线的离心率为 
