题目内容
已知p:x2-4x+3<0,q:x2-(m+1)x+m<0,(m>1).
(1)求不等式x2-4x+3<0的解集;
(2)若p是q的充分不必要条件,求m的取值范围.
解:(1)因为 ,所以
,所以 .
.
所求解集为 . ……………………………………………………… 3分
. ……………………………………………………… 3分
(2)当m >1时,
x2-(m+1)x+m<0的解是1<x<m, ………………………………………………… 5分
因为p是q的充分不必要条件,
所以x2-4x+3<0的解集是x2-(m+1)x+m<0,(m>1) 解集的真子集.
所以 . ……………………………………………………………………… 7分
. ……………………………………………………………………… 7分
当m <1时,
x2-(m+1)x+m<0的解是m <x<1,
因为p是q的充分不必要条件,
所以x2-4x+3<0的解集是x2-(m+1)x+m<0,(m<1) 解集的真子集.
因为当m <1时 ∩
∩ =Ø,
=Ø,
所以m <1时p是q的充分不必要条件不成立.
综上,m的取值范围是(3,+∞).…………………………………………………10分
解析

练习册系列答案
相关题目
已知函数 =
= ,则下列结论正确的是( )
,则下列结论正确的是( )
A.当x= 时 时 取最大值 取最大值 |
B.当x= 时 时 取最小值 取最小值 |
C.当x=- 时 时 取最大值 取最大值 |
D.当x=- 时 时 取最小值 取最小值 |

 是减函数,命题
是减函数,命题 :关于
:关于
 的解集为
的解集为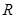 ,如果“
,如果“ 或
或 的取值范围.
的取值范围. 在区间(0,+∞)上是减函数;命题q:不等式(x-1)2>m的解集为R.若命题“p∨q”为真,命题“p∧q”为假,求实数m的取值范围是。
在区间(0,+∞)上是减函数;命题q:不等式(x-1)2>m的解集为R.若命题“p∨q”为真,命题“p∧q”为假,求实数m的取值范围是。 :函数
:函数 在区间
在区间 内不单调;命题
内不单调;命题 :当
:当 时,不等式
时,不等式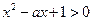 恒成立.如果命题
恒成立.如果命题
 为真命题,
为真命题,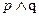 为假命题,求
为假命题,求 的取值范围.
的取值范围.
 ;
; 的充分条件,求实数
的充分条件,求实数 的取值范围。
的取值范围。 若q是p的必要不充分条件,求实数
若q是p的必要不充分条件,求实数 的取值范围。
的取值范围。 有两个不相等的实根,
有两个不相等的实根, 无实根.若同时保证:
无实根.若同时保证: 为真,
为真, 为假,求实数
为假,求实数 的取值范围。
的取值范围。 ,
,
 且
且 是
是 的充分条件,求
的充分条件,求 取值范围.
取值范围.