题目内容
给出定义:若函数 在D上可导,即
在D上可导,即 存在,且导函数
存在,且导函数 在D上也可导,则称
在D上也可导,则称 在D上存在二阶导函数,记
在D上存在二阶导函数,记 =
= ,若
,若 <0在D上恒成立,则称
<0在D上恒成立,则称 在D上为凸函数,以下四个函数在
在D上为凸函数,以下四个函数在 上不是凸函数的是( )
上不是凸函数的是( )
 在D上可导,即
在D上可导,即 存在,且导函数
存在,且导函数 在D上也可导,则称
在D上也可导,则称 在D上存在二阶导函数,记
在D上存在二阶导函数,记 =
= ,若
,若 <0在D上恒成立,则称
<0在D上恒成立,则称 在D上为凸函数,以下四个函数在
在D上为凸函数,以下四个函数在 上不是凸函数的是( )
上不是凸函数的是( ) A. = = | B. = = |
C. = = | D. = = |
B
试题分析:若
 =
= ,则
,则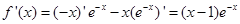 ,
,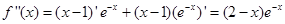 ,当
,当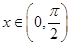 时,
时,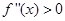 ,所以
,所以 =
= 不是凸函数。故选B。
不是凸函数。故选B。点评:本题着重考查导数的运算,因而求得公式及运算要熟悉。

练习册系列答案
相关题目
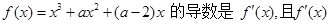 是偶函数,则曲线
是偶函数,则曲线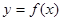 在原点处的切线方程为( )
在原点处的切线方程为( )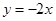
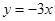
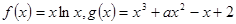
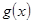 的单调递减区间为
的单调递减区间为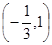 ,求函数
,求函数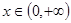 ,
,
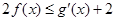 恒成立,求实数
恒成立,求实数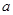 的取值范围
的取值范围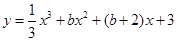 在R上不是单调递增函数,则
在R上不是单调递增函数,则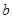 的范围是
的范围是  ,
,  .
.  时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,求函数
时,求函数 的单调区间;
的单调区间;  时,函数
时,函数 上的最大值为
上的最大值为 ,若存在
,若存在 ,使得
,使得 成立,求实数b的取值范围.
成立,求实数b的取值范围.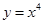 的一条切线
的一条切线 与直线
与直线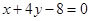 垂直,则
垂直,则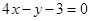
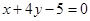
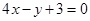
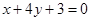
 存在导函数,则
存在导函数,则 ;②若函数
;②若函数 ,则
,则 ;③若函数
;③若函数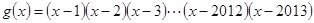 ,则
,则 ;④若三次函数
;④若三次函数 ,则“
,则“ ”是“f(x)有极值点”的充要条件;⑤函数
”是“f(x)有极值点”的充要条件;⑤函数 的单调递增区间是
的单调递增区间是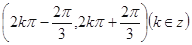 .其中真命题为____.(填序号)
.其中真命题为____.(填序号)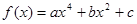 的图象经过点
的图象经过点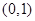 ,且在
,且在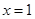 处的切线方程是
处的切线方程是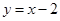
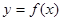 的解析式;(2)求
的解析式;(2)求 轴上一点A分别向函数
轴上一点A分别向函数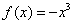 与函数
与函数 引不是水平方向的切线
引不是水平方向的切线 和
和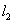 ,两切线
,两切线 轴相交于点B和点C,O为坐标原点,记△OAB的面积为
轴相交于点B和点C,O为坐标原点,记△OAB的面积为 ,△OAC的面积为
,△OAC的面积为 ,则
,则