Question

如图，在四棱锥P—ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，AB＝4，PA＝3，点A在PD上的射影为点G，点E在AB上，平面PEC⊥平面PDC.

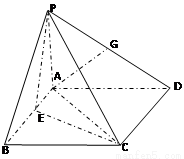
（1）求证：AG∥平面PEC；

（2）求AE的长；

（3）求二面角E—PC—A的正弦值.（本题满分14分）

 

Answer 1

【答案】

（1）见解析。（2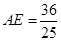）  （3）。

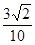【解析】       

试题分析：解（1）证明：∵CD⊥AD，CD⊥PA

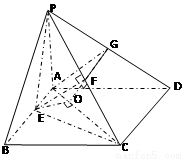
∴CD⊥平面PAD   ∴CD⊥AG，

又PD⊥AG

∴AG⊥平面PCD  ……………………2分

作EF⊥PC于F，因面PEC⊥面PCD

∴EF⊥平面PCD，

∴EF∥AG

又AG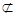面PEC，EF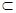面PEC，

∴AG∥平面PEC  ……………………4分

（2）由（Ⅰ）知A、E、F、G四点共面，又AE∥CD，

∴AE∥平面PCD。

∴AE∥GF。

∴四边形AEFG为平行四边形，∴AE＝GF。    ……………………………5分

∵PA＝3，AB＝4，∴PD＝5，AG＝，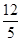

又PA²＝PG•PD，∴PG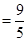     ………………………………………………7分

又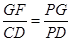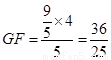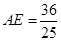，∴，∴  ………………………9分

（3）过E作EO⊥AC于点O，易知EO⊥平面PAC，

又EF⊥PC，∴OF⊥PC∴∠EFO即为二面角E—PC—A的平面角  …………11分

，

又EF＝AG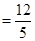

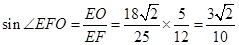∴              …………………14分

点评：二面角的求法是立体几何中的一个难点。我们解决此类问题常用的方法有两种：①综合法，综合法的一般步骤是：一作二说三求。②向量法，运用向量法求二面角应注意的是计算。很多同学都会应用向量法求二面角，但结果往往求不对，出现的问题就是计算错误。