题目内容
1.$\sqrt{2}$-1,$\frac{1}{\sqrt{2}-1}$的等差中项是$\sqrt{2}$.分析 由等差中项可得2a=$\sqrt{2}$-1+$\frac{1}{\sqrt{2}-1}$,化简根式可得a值.
解答 解:设a为$\sqrt{2}$-1,$\frac{1}{\sqrt{2}-1}$的等差中项,
则$\frac{1}{\sqrt{2}-1}$-a=a-($\sqrt{2}$-1),
∴2a=$\sqrt{2}$-1+$\frac{1}{\sqrt{2}-1}$
=$\sqrt{2}$-1+$\frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)}$
=$\sqrt{2}$-1+$\sqrt{2}$+1=2$\sqrt{2}$,
∴a=$\sqrt{2}$
故答案为:$\sqrt{2}$
点评 本题考查等差数列的通项公式,涉及根式的化简,属基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
12.$\int_{-\frac{π}{4}}^{\frac{π}{4}}{(2{{cos}^2}\frac{x}{2}+tanx)}dx$=( )
| A. | $\frac{π}{2}+\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{π}{2}$ | D. | $π+\sqrt{2}$ |
16.据如图的流程图可得结果为( )
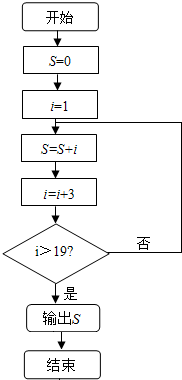

| A. | 19 | B. | 67 | C. | 51 | D. | 70 |