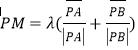题目内容
【题目】已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导数f′(x)< ![]() ,则不等式f(x2)<
,则不等式f(x2)< ![]() 的解集为 .
的解集为 .
【答案】(﹣∞,﹣1)∪(1,+∞)
【解析】解:设F(x)=f(x)﹣ ![]() x,则F′(x)=f′(x)﹣
x,则F′(x)=f′(x)﹣ ![]()
∵f′(x)< ![]() ,∴F′(x)=f′(x)﹣
,∴F′(x)=f′(x)﹣ ![]() <0
<0
即函数F(x)在R上单调递减
而f(x2)< ![]() 即f(x2)﹣
即f(x2)﹣ ![]() <f(1)﹣
<f(1)﹣ ![]()
∴F(x2)<F(1)而函数F(x)在R上单调递减
∴x2>1即x∈(﹣∞,﹣1)∪(1,+∞)
故答案为:(﹣∞,﹣1)∪(1,+∞)
设F(x)=f(x)﹣ ![]() x,根据题意可得函数F(x)在R上单调递减,然后根据f(x2)<
x,根据题意可得函数F(x)在R上单调递减,然后根据f(x2)< ![]() 可得f(x2)﹣
可得f(x2)﹣ ![]() <f(1)﹣
<f(1)﹣ ![]() ,最后根据单调性可求出x的取值范围.
,最后根据单调性可求出x的取值范围.

练习册系列答案
相关题目
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.
【题目】某班在一次个人投篮比赛中,记录了在规定时间内投进![]() 个球的人数分布情况:
个球的人数分布情况:
进球数 | 0 | 1 | 2 | 3 | 4 | 5 |
投进 | 1 | 2 | 7 | 2 |
其中![]() 和
和![]() 对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.
对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.
(1)投进3个球和4个球的分别有多少人?
(2)从进球数为3,4,5的所有人中任取2人,求这2人进球数之和为8的概率.