题目内容
在下列命题中:①若f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,θ∈(
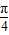 ,
,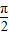 ),则f(sinθ)>f(cosθ);
),则f(sinθ)>f(cosθ);②若锐角α、β满足cosα>sinβ,则α+β<
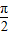 ;
;③若f(x)=2cos2
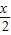 -1,则f(x+π)=f(x)对x∈R恒成立;
-1,则f(x+π)=f(x)对x∈R恒成立;④对于任意实数a,要使函数y=5cos(
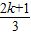 πx-
πx-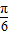 )(k∈N*)在区间[a,a+3]上的值
)(k∈N*)在区间[a,a+3]上的值 出现的次数不小于4次,又不多于8次,则k可以取2和3.
出现的次数不小于4次,又不多于8次,则k可以取2和3. 其中真命题的序号是 .
【答案】分析:①由偶函数对称区间上的单调性相反可知,函数在[0,1]上单调递减,结合θ∈(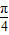 ,
,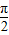 )时,可判断sinθ与cosθ的大小,进而可比较
)时,可判断sinθ与cosθ的大小,进而可比较
②由锐角α、β满足cosα>sinβ=cos( ),可判断
),可判断
③f(x)=2cos2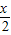 -1=cosx,函数的周期为T=2π,可判断
-1=cosx,函数的周期为T=2π,可判断
④由于函数y=5cos( πx-
πx-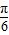 )在一个周期内函数值
)在一个周期内函数值 出现两次,若满在区间[a,a+3]上的值
出现两次,若满在区间[a,a+3]上的值 出现的次数不小于4次,又不多于8次,则用检验当k=2,3时函数的周期即可判断
出现的次数不小于4次,又不多于8次,则用检验当k=2,3时函数的周期即可判断
解答:解:①由偶函数对称区间上的单调性相反可知,函数在[0,1]上单调递减,又θ∈(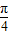 ,
,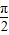 )时,1>sinθ>cosθ>0,则f(sinθ)∠f(cosθ);故①错误
)时,1>sinθ>cosθ>0,则f(sinθ)∠f(cosθ);故①错误
②若锐角α、β满足cosα>sinβ=cos(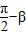 ),则
),则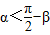 ,则α+β<
,则α+β<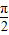 ;②正确
;②正确
③f(x)=2cos2 -1=cosx,函数的周期为T=2π,则f(x+π)=f(x)对x∈R恒成立;③错误
-1=cosx,函数的周期为T=2π,则f(x+π)=f(x)对x∈R恒成立;③错误
④由于函数y=5cos(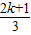 πx-
πx- )在一个周期内函数值
)在一个周期内函数值 出现两次,若满在区间[a,a+3]上的值
出现两次,若满在区间[a,a+3]上的值 出现的次数不小于4次,又不多于8次,则
出现的次数不小于4次,又不多于8次,则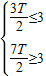
当k=2时,周期T= ,则函数y=5cos(
,则函数y=5cos(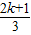 πx-
πx-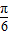 )在区间[a,a+3]内函数值
)在区间[a,a+3]内函数值 出现6次,满足题意
出现6次,满足题意
当k=3时,周期T= ,则函数y=5cos(
,则函数y=5cos(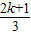 πx-
πx-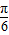 )在区间[a,a+3]内函数值
)在区间[a,a+3]内函数值 出现最大出现8次,满足题意;故④正确
出现最大出现8次,满足题意;故④正确
故答案为:②④
点评:本题综合考查了偶函数的对称区间上的单调性的应用,三角函数的诱导公式的应用,函数的周期公式的应用及二倍角公式、余弦函数的性质等函数知识的综合应用
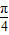 ,
,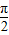 )时,可判断sinθ与cosθ的大小,进而可比较
)时,可判断sinθ与cosθ的大小,进而可比较②由锐角α、β满足cosα>sinβ=cos(
 ),可判断
),可判断③f(x)=2cos2
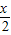 -1=cosx,函数的周期为T=2π,可判断
-1=cosx,函数的周期为T=2π,可判断④由于函数y=5cos(
 πx-
πx-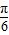 )在一个周期内函数值
)在一个周期内函数值 出现两次,若满在区间[a,a+3]上的值
出现两次,若满在区间[a,a+3]上的值 出现的次数不小于4次,又不多于8次,则用检验当k=2,3时函数的周期即可判断
出现的次数不小于4次,又不多于8次,则用检验当k=2,3时函数的周期即可判断解答:解:①由偶函数对称区间上的单调性相反可知,函数在[0,1]上单调递减,又θ∈(
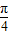 ,
,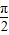 )时,1>sinθ>cosθ>0,则f(sinθ)∠f(cosθ);故①错误
)时,1>sinθ>cosθ>0,则f(sinθ)∠f(cosθ);故①错误②若锐角α、β满足cosα>sinβ=cos(
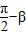 ),则
),则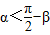 ,则α+β<
,则α+β<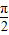 ;②正确
;②正确③f(x)=2cos2
 -1=cosx,函数的周期为T=2π,则f(x+π)=f(x)对x∈R恒成立;③错误
-1=cosx,函数的周期为T=2π,则f(x+π)=f(x)对x∈R恒成立;③错误④由于函数y=5cos(
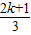 πx-
πx- )在一个周期内函数值
)在一个周期内函数值 出现两次,若满在区间[a,a+3]上的值
出现两次,若满在区间[a,a+3]上的值 出现的次数不小于4次,又不多于8次,则
出现的次数不小于4次,又不多于8次,则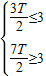
当k=2时,周期T=
 ,则函数y=5cos(
,则函数y=5cos(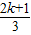 πx-
πx-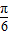 )在区间[a,a+3]内函数值
)在区间[a,a+3]内函数值 出现6次,满足题意
出现6次,满足题意 当k=3时,周期T=
 ,则函数y=5cos(
,则函数y=5cos(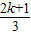 πx-
πx-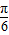 )在区间[a,a+3]内函数值
)在区间[a,a+3]内函数值 出现最大出现8次,满足题意;故④正确
出现最大出现8次,满足题意;故④正确故答案为:②④
点评:本题综合考查了偶函数的对称区间上的单调性的应用,三角函数的诱导公式的应用,函数的周期公式的应用及二倍角公式、余弦函数的性质等函数知识的综合应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目