题目内容
在下列命题中,所有正确命题的序号是
①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x<0”;
②若p是q的充分不必要条件,则?p是?q的必要不充分条件;
③函数f(x)=lg(x2+x+a)的值域为R的充要条件是a≤
;
④若函数f(x)=
在(1,+∞)内为增函数,则a<2.
②③
②③
.①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x<0”;
②若p是q的充分不必要条件,则?p是?q的必要不充分条件;
③函数f(x)=lg(x2+x+a)的值域为R的充要条件是a≤
| 1 |
| 4 |
④若函数f(x)=
| 2x-a |
| x-1 |
分析:对于①,命题的否定量词与结论都进行否定;对于②,根据原命题与逆否命题的等价性;
对于③,函数f(x)=lg(x2+x+a)的值域为R,则△=1-4a≥0;对于④,f(x)=
=2+
,则2-a>0,从而可得结论.
对于③,函数f(x)=lg(x2+x+a)的值域为R,则△=1-4a≥0;对于④,f(x)=
| 2x-a |
| x-1 |
| 2-a |
| x-1 |
解答:解:对于①,命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”,故不正确;
对于②,根据原命题与逆否命题的等价性,可知结论正确;
对于③,函数f(x)=lg(x2+x+a)的值域为R,则△=1-4a≥0,∴a≤
,故结论正确;
对于④,f(x)=
=2+
,∵函数f(x)=
在(1,+∞)内为增函数,∴2-a<0,∴a>2,故结论不正确;
综上知,正确命题的序号是②③
故答案为:②③
对于②,根据原命题与逆否命题的等价性,可知结论正确;
对于③,函数f(x)=lg(x2+x+a)的值域为R,则△=1-4a≥0,∴a≤
| 1 |
| 4 |
对于④,f(x)=
| 2x-a |
| x-1 |
| 2-a |
| x-1 |
| 2x-a |
| x-1 |
综上知,正确命题的序号是②③
故答案为:②③
点评:本题综合考查命题的否定,考查四种条件,考查函数的单调性,解题时需要一一加以判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
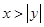 ”是“
”是“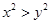 ”的充要条件;
”的充要条件; 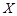 服从正态分布
服从正态分布 ,
,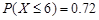 ,则
,则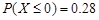 ;
;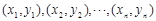 的散点图都在直线
的散点图都在直线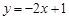 上,则这n组数据的相关系数为
上,则这n组数据的相关系数为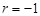 ;
;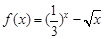 的所有零点存在区间是
的所有零点存在区间是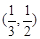 .其中正确的个数是( )
.其中正确的个数是( )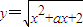 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2];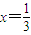 对称.
对称.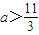 ;
;