题目内容

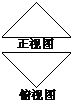
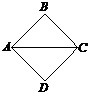精英家教网精英家教网将边长为1的正方形ABCD沿对角线AC折叠，其正视图和俯视图如图所示．此时连接顶点B、D形成三棱锥B-ACD，则其侧视图的面积为（　　）
A、1
B、
1
2
C、
1
4
D、
1
8
分析：根据原来的正方形和正视图和俯视图可知，平面ABC与平面ACD垂直，三棱锥B-ACD侧视图为等腰直角三角形，根据长度做出侧视图的面积．
解答：解：由正视图和俯视图可知，
平面ABC⊥平面ACD．
三棱锥B-ACD侧视图为等腰直角三角形，
直角边长为
2
2
，
∴侧视图面积为
1
4
．
故选C．
点评：本题考查简单空间图形的三视图，考查根据原图与另外的三视图，确定第三个三视图的形状，本题是一个基础题．
练习册系列答案
相关题目
将边长为1的正方形ABCD沿对角线BD折起，使得点A到点A′的位置，且A′C=1，则折起后二面角A′-DC-B的大小（　　）
A、arctan
2
2
B、
π
4
C、arctan
2
D、
π
3
精英家教网将边长为1的正方形ABCD沿对角线BD折成直二面角，若点P满足
BP
=
1
2
BA
-
1
2
BC
+
BD
，则|
BP
|2的值为（　　）
A、
3
2
B、2
C、
10-
2
4
D、
9
4
将边长为1的正方形ABCD沿对角线AC折起，使得平面ADC⊥平面ABC，在折起后形成的三棱锥D-ABC中，给出下列三个命题：
①面DBC是等边三角形；  ②AC⊥BD；  ③三棱锥D-ABC的体积是
2
6
．
其中正确命题的个数为（　　）
将边长为1的正方形ABCD沿对角线BD折起成直二面角A-BD-C，则在这个直二面角A-BD-C中点A到直线BC的距离是
3
2
3
2
．
将边长为1的正方形ABCD沿对角线AC对折成120°的二面角，则B、D在四面体A-BCD的外接球球面上的距离为
2
π
3
2
π
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网