题目内容
将边长为1的正方形ABCD沿对角线BD折起成直二面角A-BD-C,则在这个直二面角A-BD-C中点A到直线BC的距离是
.
| ||
| 2 |
| ||
| 2 |
分析:根据题意,先作出表示A到直线BC的距离的线段,再在直角三角形中进行求解即可
解答: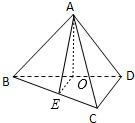 解:分别取BD,BC的中点O,E,连接AO,OE,AE
解:分别取BD,BC的中点O,E,连接AO,OE,AE
∵ABCD是正方形
∴AO⊥BD
∵A-BD-C是直二面角,平面ABD∩平面BCD=BD
∴AO⊥平面BDC
∴E是BC的中点
∴OE⊥BC
∴AE⊥BC
∴AE表示A到直线BC的距离
∵AB=1,BE=
∴AE=
∴A到直线BC的距离为
故答案为:
 解:分别取BD,BC的中点O,E,连接AO,OE,AE
解:分别取BD,BC的中点O,E,连接AO,OE,AE∵ABCD是正方形
∴AO⊥BD
∵A-BD-C是直二面角,平面ABD∩平面BCD=BD
∴AO⊥平面BDC
∴E是BC的中点
∴OE⊥BC
∴AE⊥BC
∴AE表示A到直线BC的距离
∵AB=1,BE=
| 1 |
| 2 |
∴AE=
| ||
| 2 |
∴A到直线BC的距离为
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查与二面角有关立体几何中点线之间距离的计算,考查学生对空间图形的理解,属于基础题.

练习册系列答案
相关题目
将边长为1的正方形ABCD沿对角线BD折起,使得点A到点A′的位置,且A′C=1,则折起后二面角A′-DC-B的大小( )
A、arctan
| ||||
B、
| ||||
C、arctan
| ||||
D、
|
 将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足
将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足| BP |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| BC |
| BD |
| BP |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|