题目内容
已知动点P(x,y)与一定点F(1,0)的距离和它到一定直线l:x=4的距离之比为
.
(Ⅰ) 求动点P(x,y)的轨迹C的方程;
(Ⅱ)已知直线l':x=my+1交轨迹C于A、B两点,过点A、B分别作直线l:x=4的垂线,垂足依次为点D、E.连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;否则说明理由.
| 1 |
| 2 |
(Ⅰ) 求动点P(x,y)的轨迹C的方程;
(Ⅱ)已知直线l':x=my+1交轨迹C于A、B两点,过点A、B分别作直线l:x=4的垂线,垂足依次为点D、E.连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;否则说明理由.
(Ⅰ)由题意得
=
,
即2
=|x-4|,
两边平方得:4x2-8x+4+4y2=x2-8x+16.
得
+
=1.
所以动点P(x,y)的轨迹C的方程为椭圆
+
=1.
(Ⅱ)当m变化时,直线AE、BD相交于一定点N(
,0).
证明:如图,
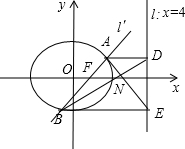
当m=0时,联立直线x=1与椭圆
+
=1,
得A(1,
)、B(1,-
),
过A、B作直线x=4的垂线,得两垂足D(4,
)、E(4,-
).
由直线方程的两点式得:直线AE的方程为:2x+2y-5=0,直线BD的方程为:2x-2y-5=0,
方程联立解得x=
,y=0,所以直线AE、BD相交于一点(
,0).
假设直线AE、BD相交于一定点N(
,0).
证明:设A(my1+1,y1),B(my2+1,y2),则D(4,y1),E(4,y2),
由
消去x并整理得(3m2+4)y2+6my-9=0,
△=36m2-4×(3m2+4)×(-9)=144m2+144>0>0,
由韦达定理得y1+y2=
,y1y2=
.
因为
=(my1-
,y1),
=(
,y2),
所以(my1-
)×y2-y1×
=my1y2-
(y1+y2)=
-
×
=0
所以,
∥
,所以A、N、E三点共线,
同理可证B、N、D三点共线,所以直线AE、BD相交于一定点N(
,0).
| ||
| |x-4| |
| 1 |
| 2 |
即2
| (x-1)2+y2 |
两边平方得:4x2-8x+4+4y2=x2-8x+16.
得
| x2 |
| 4 |
| y2 |
| 3 |
所以动点P(x,y)的轨迹C的方程为椭圆
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)当m变化时,直线AE、BD相交于一定点N(
| 5 |
| 2 |
证明:如图,

当m=0时,联立直线x=1与椭圆
| x2 |
| 4 |
| y2 |
| 3 |
得A(1,
| 3 |
| 2 |
| 3 |
| 2 |
过A、B作直线x=4的垂线,得两垂足D(4,
| 3 |
| 2 |
| 3 |
| 2 |
由直线方程的两点式得:直线AE的方程为:2x+2y-5=0,直线BD的方程为:2x-2y-5=0,
方程联立解得x=
| 5 |
| 2 |
| 5 |
| 2 |
假设直线AE、BD相交于一定点N(
| 5 |
| 2 |
证明:设A(my1+1,y1),B(my2+1,y2),则D(4,y1),E(4,y2),
由
|
△=36m2-4×(3m2+4)×(-9)=144m2+144>0>0,
由韦达定理得y1+y2=
| -6m |
| 3m2+4 |
| -9 |
| 3m2+4 |
因为
| NA |
| 3 |
| 2 |
| NE |
| 3 |
| 2 |
所以(my1-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| -9m |
| 3m2+4 |
| 3 |
| 2 |
| -6m |
| 3m2+4 |
所以,
| NA |
| NE |
同理可证B、N、D三点共线,所以直线AE、BD相交于一定点N(
| 5 |
| 2 |

练习册系列答案
相关题目